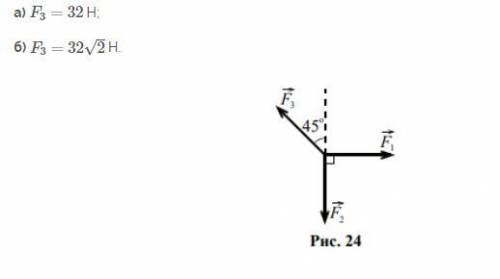
На тело действуют три силы (рис. 24), лежащие в одной плоскости. Известно, что F1 = F2 = 32H. Найти равнодействующую силу (модуль, направление и точку приложения) для двух случаев:
Другие вопросы по теме Физика
Популярные вопросы
- Какое число больше или меньше: a или p (a≠0; p≠0) — если: a+4=p? ответ (для записи...
3 - Love, broadcast, compose, sing, not speak, become, appear, finish, win....
1 - Сочинение на тему каменный цветок. чему может нас научить рассказ бажова...
2 - Укажи предложение(-я) с простым глагольным сказуемым. устинья яковлевна поднесла...
3 - Написать сочинение на тему владимир дубровский и маша троекурова + план (если...
2 - Боги финикийцев покровительствовали мелькарт - городэшмун - город астрата - город...
2 - 1. қанның формалы элементтерін белгілеңіз.a) су және минералды тұздарb) қан плазмасындағы...
2 - Какие подвиги совершал гайавата...
1 - Cколько существует двухзначных чисел кратных 11 но не кратных 33...
1 - Сочинение - рассуждение на тему: какого человека можно назвать смелым? 1)что такое...
2
F₁ = F₂ = 32 H
a)
F₃ = 32 H
б)
F₃ = 32√2 H
-----------------------------------------------------
R - ? - равнодействующая системы сил
α - ? - угол наклона к горизонтали
Точка приложения - ?
-------------------------------------------------------
Выберем систему координат:
начало координат О - в точке приложения всех трёх сил;
ось Ох - направлена вдоль линии действия силы F₁, то есть вправо по горизонтали;
ось Оу - направлена в направлении. противоположном направлению силы F₂, то есть вертикально вверх.
Точка приложения равнодействующей - начало координат - точка О
Проекция равнодействующей R системы сил F₁, F₂, F₃ на ось Ох
Проекция равнодействующей R системы сил F₁, F₂, F₃ на ось Оy
Модуль |R| равнодействующей системы сил F₁, F₂, F₃
Угол между вектором равнодействующей R и горизонтальной осью Ох
a)
б)
Система сил уравновешена, так как R = 0