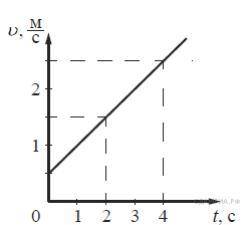
На рисунке представлен график зависимости скорости тела от времени. Во сколько раз увеличится модуль импульса тела за время от 2

до 4 секунд?

Для решения данной задачи, нам необходимо определить первоначальное значение импульса тела в момент времени t1 = 2 сек и окончательное значение импульса тела в момент времени t2 = 4 сек.

Импульс тела определяется как произведение массы тела на его скорость. В данной задаче мы не имеем информации о массе тела, поэтому предположим, что масса остается постоянной.

Поскольку у нас дан график зависимости скорости тела от времени, мы можем использовать описание площади под графиком, чтобы найти интересующее нас изменение импульса.

Для начала, найдем площадь под графиком скорости от t1 до t2. Мы можем разделить эту площадь на площадь под самим графиком скорости при t1, чтобы найти во сколько раз площадь под графиком увеличится за заданный промежуток времени.

Для удобства, давайте разобьем общий промежуток времени от 0 до 4 сек на два промежутка: от 0 до 2 сек и от 2 до 4 сек.

Применим формулу для площади под графиком, она равна интегралу от функции скорости по времени на заданном интервале.

Площадь под графиком скорости от 0 до 2 сек будет равна интегралу от 0 до 2 функции скорости. Если рассмотреть вид графика, можно заметить, что это площадь треугольника плюс площадь прямоугольника.

Площадь треугольника можно найти, умножив половину длины основания (2 сек) на высоту (8 м/с), то есть 1 * 8 = 8 кг*м/с.

Площадь прямоугольника можно найти, умножив длину основания (2 сек) на ширину (6 м/с), то есть 2 * 6 = 12 кг*м/с.

Общая площадь под графиком от 0 до 2 сек будет равна сумме площади треугольника и площади прямоугольника, 8 + 12 = 20 кг*м/с.

Теперь найдем площадь под графиком скорости от 2 до 4 сек. Опять можно заметить, что это площадь треугольника плюс площадь прямоугольника.

По аналогии с предыдущим расчетом, площадь треугольника равна 1 * 4 = 4 кг*м/с, а площадь прямоугольника равна 2 * 4 = 8 кг*м/с. Общая площадь под графиком от 2 до 4 сек будет равна 4 + 8 = 12 кг*м/с.

Теперь, чтобы найти во сколько раз площадь под графиком увеличилась от t1 до t2, нам нужно разделить площадь от 2 до 4 сек на площадь от 0 до 2 сек: 12 / 20 = 0.6.

Итак, модуль импульса тела увеличится примерно в 0.6 раза за время от 2 до 4 секунд.