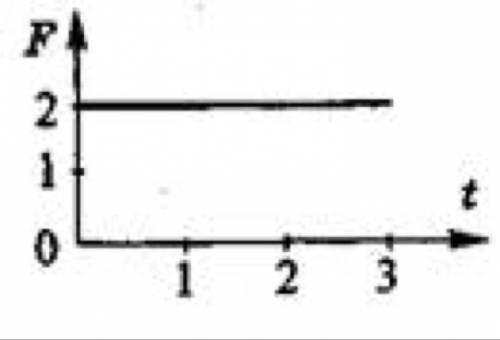
На рисунке представлен график зависимости модуля равнодейст­вующей всех сил, действующих на тело, от времени. Чему равно из­менение импульса тела в проме­жуток времени от первой до третьей секунды?

Решение: f2\f1=s2\s1⇒f2=f1×s2\s1 f2=18000h×4см2\180см2=400н надеюсь .

Чтобы решить задачу, нам необходимо определить площадь под графиком в интервале от первой до третьей секунды. Поскольку график представляет зависимость модуля равнодействующей всех сил от времени, площадь под графиком будет равна изменению импульса тела за указанный промежуток времени.

Для нахождения площади под графиком, можно разделить область под графиком на прямоугольники и треугольники, а затем сложить площади этих фигур.

1. Область под графиком ограничена осью времени (ось x) и графиком самим собой.
2. Для простоты, мы можем считать, что график состоит из треугольников и прямоугольников.
3. Измерим высоту прямоугольников и треугольников на графике.
4. Вычислим площади этих фигур и сложим их, чтобы получить общую площадь под графиком.

На графике видны два прямоугольника и два треугольника.

1. Первый прямоугольник: его высота составляет 5 N, а его ширина равна 1 секунде. Поэтому его площадь равна 5 N × 1 сек = 5 Н·с.

2. Первый треугольник: его высота составляет 5 N, а его основание равно 1 секунде. Поэтому его площадь равна 1/2 × 5 N × 1 сек = 2.5 Н·с.

3. Второй прямоугольник: его высота составляет 2 N, а его ширина равна 1 секунде. Таким образом, его площадь равна 2 N × 1 сек = 2 Н·с.

4. Второй треугольник: его высота составляет 2 N, а его основание равно 1 секунде. Поэтому его площадь составляет 1/2 × 2 N × 1 сек = 1 Н·с.

Теперь сложим площади прямоугольника и треугольников:
5 Н·с + 2.5 Н·с + 2 Н·с + 1 Н·с = 10.5 Н·с.

Изменение импульса тела в течение указанного периода времени (от первой до третьей секунды) равно 10,5 Н·с (ньютон-секунд).