на рисунке 92 представлен график зависимости проекции скорости движения шайбы, скользящий по горизонтальному льду, от времени. Определите коэффициент трения между шайбой и льдом.
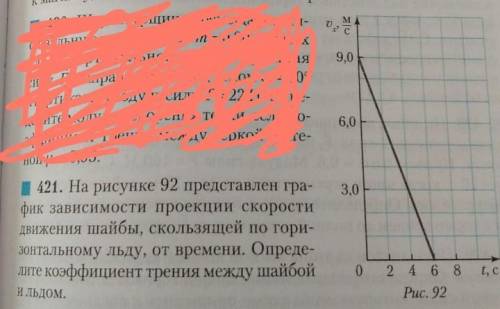
Другие вопросы по теме Физика
Популярные вопросы
- При каких значениях переменной имеет смысл выражения ...
2 - На фотке всёёёёёёёёёёёёёёёёёёёёёё...
1 - Письменно ответьте на во Как вы думаете, что может быть ценно для человека,...
2 - Терміново. Завдання на фото...
2 - У давніх слов ян роль товарних грошей часто належала? А. скляним виробамБ. перламВ....
2 - Записать дифференциал 2-го порядка функции двух переменных. z=e^xy...
2 - У трикутнику АВС відомо,що АВ АС,АВ=ВС. Укажіть правільне твердження...
3 - При титровании 15 мл раствора азотной кислоты израсходовано 20 мл раствора гидроксида...
2 - Выясните, при каком значении ртрехчлен pH бр - 1 принимаетнаименьшее значение...
3 - Сформулируйте и запишите вывод о том, как меняется изображение при удалении...
3
Fтр = μ * N
где Fтр - сила трения, μ - коэффициент трения, N - нормальная реакция опоры.
На графике представлена проекция скорости шайбы, которая является производной координаты по времени, т.е. скорость = dx/dt. Для нахождения значения коэффициента трения мы можем воспользоваться участком графика, на котором скорость движения шайбы постоянна, так как на этом участке трение считается статическим.
На графике примерно до t=0.5 секунды проекция скорости шайбы равна 20 м/с. Это и будет скорость, с которой шайба двигается при статическом трении. Теперь нам нужно определить нормальную реакцию опоры. В данном случае, так как движение происходит по горизонтальной поверхности, нормальная реакция опоры должна быть равна силе тяжести:
N = mg
где m - масса шайбы, g - ускорение свободного падения.
Эту формулу можно использовать, так как сила тяжести направлена вертикально вниз и при движении по горизонтальной поверхности не создает горизонтальную силу.
Для простоты в расчетах, предположим, что масса шайбы равна 1 кг, а ускорение свободного падения g = 9.8 м/с^2.
Теперь мы можем найти нормальную реакцию опоры:
N = 1 кг * 9.8 м/с^2 = 9.8 Н
Теперь, подставив найденные значения в уравнение для трения, мы можем найти коэффициент трения:
Fтр = μ * N
20 м/с^2 = μ * 9.8 Н
μ = 20 м/с^2 / 9.8 Н ≈ 2.04
Таким образом, коэффициент трения между шайбой и льдом составляет около 2.04.
Важно отметить, что коэффициент трения между шайбой и льдом может изменяться в разных условиях, например, при изменении поверхности льда, состояния шайбы и других факторов. Поэтому результаты данного расчета применимы только для данного конкретного эксперимента.