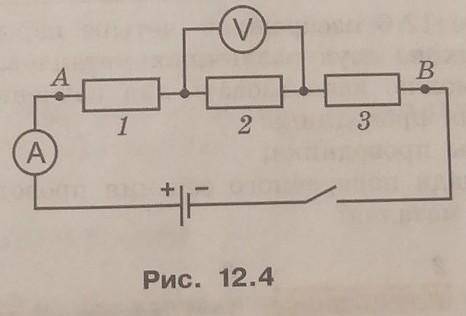
На рисунке 12.4 изображена схема электрической цепи в которую включены резисторы сопротивлениями R1=5 Ом, R2=6 Ом и R3=12 Ом вольтметр показывает 1,2В Какую силу тока показывает амперметр и чему равно напряжение между точками A и B??​

Чтобы решить эту задачу, мы можем использовать закон Ома, который гласит, что сила тока (I) в электрической цепи равна отношению напряжения (U) к сопротивлению (R): I = U/R.

Нам дано значение напряжения между точками A и B, равное 1,2 В. Мы также знаем значения сопротивлений резисторов R1, R2 и R3, которые равны соответственно 5 Ом, 6 Ом и 12 Ом.

Теперь нам нужно найти силу тока, показываемую амперметром. Для этого нам необходимо вычислить эквивалентное сопротивление всей цепи. В электрической цепи резисторы соединяются последовательно и параллельно.

Первым шагом мы можем объединить резисторы R1 и R2, так как они соединены последовательно. Это означает, что их сопротивления суммируются: R1 + R2 = 5 Ом + 6 Ом = 11 Ом.

Теперь у нас есть новое сопротивление, которое можно обозначить как R12, и оно параллельно связано с резистором R3. Мы можем использовать следующую формулу для расчета эквивалентного сопротивления для резисторов, соединенных параллельно: 1/R_equiv = 1/R12 + 1/R3.

Подставляя значения, получим: 1/R_equiv = 1/11 Ом + 1/12 Ом. После упрощения дроби получим: 1/R_equiv = (12 + 11)/(11 * 12) = 23/132.

Теперь, чтобы найти R_equiv, нам нужно взять обратное значение эквивалентного сопротивления: R_equiv = 132/23 Ом.

Мы нашли эквивалентное сопротивление всей цепи, теперь мы можем использовать закон Ома, чтобы найти силу тока. Подставляем значения в формулу: I = U/R_equiv = 1,2 В / (132/23) Ом.

Для упрощения вычисления, мы умножаем числитель и знаменатель второй дроби на 23: I = 1,2 В * (23/132) Ом.

Теперь вычисляем: I = 1,2 В * 23 / 132 Ом = 0,2091 А (округляем до четырех знаков после запятой).

Таким образом, сила тока, показываемая амперметром, составляет примерно 0,2091 А.

Чтобы найти напряжение между точками A и B, мы можем использовать закон Ома в отношении сопротивления R3, так как напряжение показывается вольтметром, который подключен к этому резистору.

Подставляем значения в формулу: U_AB = I * R3 = 0,2091 А * 12 Ом.

Вычисляем: U_AB = 2,5092 В (округляем до четырех знаков после запятой).

Таким образом, напряжение между точками A и B составляет примерно 2,5092 В.