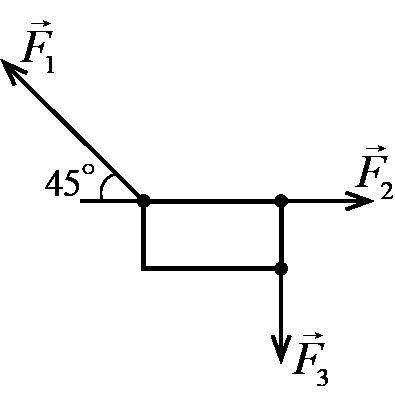
На прямоугольную пластину в её плоскости действуют силы `F_3=F_2=17` H, `F_1=17sqrt2` H. Покажите, что у такой системы сил нет равнодействующей. Опишите качественно начальный характер движения пластины под действием этих сил из неподвижного состояния.

Для начала рассмотрим силы, действующие на пластину. У нас имеется три силы: F₁, F₂ и F₃. F₁ и F₂ действуют по диагонали прямоугольника, а F₃ действует по горизонтали.

Для того чтобы увидеть, есть ли равнодействующая сил на пластину, нужно сложить все векторные силы вместе, используя метод параллелограмма. Для этого нарисуем векторы F₁ и F₂ так, чтобы их концы соединялись с началом F₃. Образовавшийся параллелограмм имеет диагональ, которая и будет равнодействующей силы.

В нашем случае, поскольку F₁ = F₂ = 17 H, мы можем представить F₁ и F₂ как две стороны квадрата. Так как две соседние стороны квадрата образуют угол 90 градусов, соединение начала F₃ с концом F₁ и F₂ образует прямоугольный треугольник.

Далее, используя теорему Пифагора, мы можем найти длину диагонали, которая равна равнодействующей силы. В нашем случае, применение теоремы Пифагора к прямоугольному треугольнику даёт нам √(17² + 17²) = √(2 * 17²) = 17√2 H.

Таким образом, мы видим, что длина диагонали параллелограмма (равнодействующая сила) равна 17√2 H, что означает наличие этих сил.

Теперь давайте рассмотрим начальный характер движения пластины под действием этих сил из неподвижного состояния. У нас есть две равных по величине силы F₁ и F₂, которые действуют под углами 45 градусов к плоскости пластины. Их векторная сумма (равнодействующая сила) имеет направление под углом 45 градусов к F₃. То есть, пластина будет двигаться вдоль диагонали прямоугольника, образованного F₁ и F₂.

Так как F₃ действует горизонтально, пластина также будет двигаться параллельно горизонтальной оси, но с некоторой наклонной составляющей, обусловленной действием F₁ и F₂. Движение будет происходить в направлении от начала F₃ к его концу, так как равнодействующая сила направлена в эту сторону.

В итоге, пластина будет двигаться по диагонали прямоугольника, образованного F₁ и F₂, и при этом будет иметь горизонтальную составляющую из-за действия F₃.