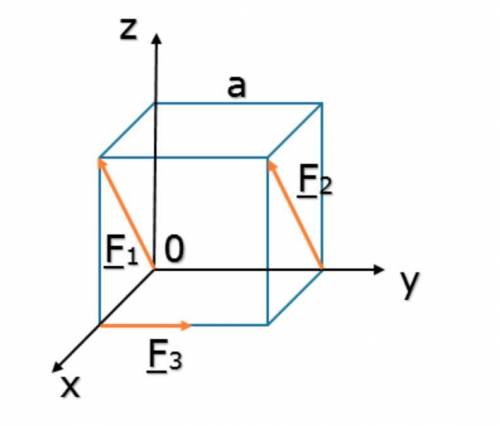
На куб с ребром а = 0,8 м действуют силы F1 = F2 = 4 Н и F3 = 3 Н. Определить модуль главного момента этих сил, выбрав за центр приведения точку О. На куб с ребром а = 1 м действует сила F = 1 кН и пара сил с моментом М = 5 кН·м. Определить главный момент в кН·м данной системы сил, приняв за центр приведения точку О.

Физика требует жерт

Добрый день! Рассмотрим каждый из вопросов по очереди:

1. На куб с ребром a = 0,8 м действуют силы F1 = F2 = 4 Н и F3 = 3 Н. Нам нужно определить модуль главного момента этих сил, выбрав за центр приведения точку О.

Для начала, определим момент каждой силы относительно точки O. Моментом силы называется векторная величина, равная произведению модуля силы на перпендикулярное ей расстояние до точки O.

Для определения модуля момента силы можно использовать формулу M = F * d * sin(α), где M - модуль момента силы, F - модуль силы, d - расстояние от точки O до линии действия силы, α - угол между линией действия силы и линией, проведенной от точки O до этой линии.

Для сил F1 и F2 модули моментов будут одинаковыми, так как они действуют в одной плоскости и расстояние до точки O одинаковое. Поэтому найдем модуль момента только для одной из сил.

Поскольку Ф1 = Ф2 = 4 Н, то модуль момента для каждой из них будет равен:
М1 = М2 = 4 Н * d * sin(α)

Заметим, что углы α и β (как на рисунке) являются смежными, поэтому α + β = 90°. Из этого следует, что sin(α) = cos(β).

Так как куб является геометрическим телом с симметричной структурой, расстояние d будет равно половине его ребра. В данном случае d = a/2 = 0,8 м / 2 = 0,4 м.

Теперь можем рассчитать модуль момента для обеих сил:
М1 = М2 = 4 Н * 0,4 м * sin(α) = 4 Н * 0,4 м * cos(β)

Теперь необходимо определить модуль момента для силы F3. Для этого воспользуемся той же формулой:

М3 = 3 Н * d * sin(β)

Так как sin(β) = cos(α), то можно записать:
М3 = 3 Н * 0,4 м * cos(α)

Таким образом, модуль главного момента этих сил будет равен сумме модулей моментов каждой из сил:
Мглавн = М1 + М2 + М3
Мглавн = 4 Н * 0,4 м * cos(β) + 4 Н * 0,4 м * cos(β) + 3 Н * 0,4 м * cos(α)
Мглавн = 8 Н * 0,4 м * cos(β) + 3 Н * 0,4 м * cos(α)

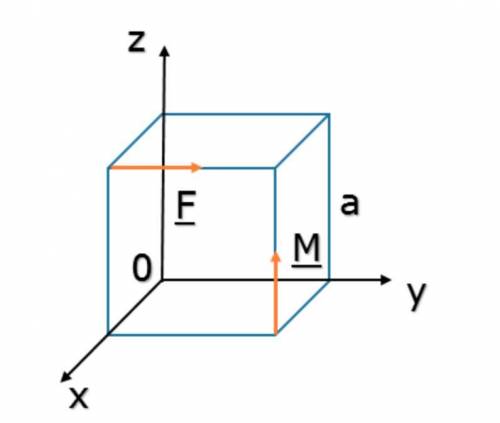
2. На куб с ребром a = 1 м действует сила F = 1 кН и пара сил с моментом М = 5 кН·м. Нам нужно определить главный момент в кН·м данной системы сил, приняв за центр приведения точку О.

В данном случае уже дано значение момента пары сил М = 5 кН·м и силы F = 1 кН.

Главный момент системы сил можно определить как сумму момента силы F и момента пары сил.

Мглавн = М + F * d * sin(α)

Для определения модуля момента пары сил, используем формулу М = F * d, где F - модуль одной из сил пары и d - расстояние от точки O до оси сил пары.

Так как у нас задана пара сил с модулем момента М = 5 кН·м, можем записать:
5 кН·м = F * d

Теперь можем решить это уравнение относительно расстояния d:
d = 5 кН·м / F

Итак, расстояние d будет равно:
d = 5 кН·м / 1 кН = 5 м

Теперь можем рассчитать модуль главного момента системы сил:
Мглавн = 5 кН·м + 1 кН * 5 м * sin(α)
Мглавн = 5 кН·м + 5 кН * 5 м * sin(α)
Мглавн = 5 кН·м + 25 кН·м * sin(α)

Это и есть ответ на второй вопрос.

Надеюсь, я ответил на ваш вопрос достаточно подробно и понятно для школьника. Если возникнут еще вопросы, не стесняйтесь задавать!