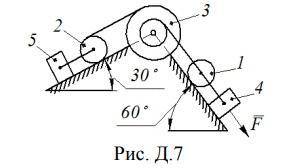
Механическая система состоит из тел 1, 2, …5 массами m1, m2, … m5, связанных
друг с другом нитями, намотанными на ступенчатый блок 3 (рис. Д.0–Д.9). Участки
нитей параллельны плоскостям, грузы скользят по плоскостям без трения, а катки
катятся без скольжения.
Радиусы ступенчатого блока 3 равны соответственно
R3 R
;
r3 0,5R
и радиус
катков ri = 0,5R, где R = 0,5 м. При вычислении моментов инерции блок и катки считать
однородными сплошными цилиндрами радиуса R и ri соответственно. На систему, кроме
сил тяжести, действует сила F, приложенная к соответствующему телу и пара сил
сопротивления M, приложенных к блоку 3.
Прочерк в столбцах таблицы 3, где заданы массы, означает, что соответствующее
тело в систему не входит (на рисунке не изображать), а ноль – тело считается невесомым,
но в систему входит. В начальный момент система находилась в покое.
Определить значение искомой величины, указанной в столбце «Найти», где
i –
угловая скорость тела, vi – скорость центра масс тела, в момент времени, когда блок 3
повернется на угол φ в направлении действия силы F. Индекс i означает номер тела.
m1=2; m2=0; m3=4;m5=3 (кг); М=8 (Н*м) F=200Н;угол фи= 60 град; найти угловую скорость омега3
Другие вопросы по теме Физика
Популярные вопросы
- В романе представлены образы европейских королей. С какой целью они введены...
3 - 172. (в15-116-14) Определите существительные женского рода:1) манго; 2) невежа;...
1 - При нормальных условиях одинаковый молярный объем имеют: 1)водород и кислород2)бром...
2 - заполнить таблицу с функций. Задания на фото:...
3 - Составьте отрицательное предложение из приведенных ниже слов. EATING ARE SOUP...
1 - Родственные тональности к ля минору...
1 - Спишите текст, соблюдая орфографические и пунктуационные нормы. Обозначьте...
3 - N=5 На основании нижеприведенных данных провести анализ движения рабочей силы....
3 - Если наполнять бассейн одной трубой, то бассейн наполнится за 20 минут, а если...
2 - I the poem in two days A)translateB)translatesC)translatedD)was translatingE)shall...
1
Шаг 1: Найдем силы реакции нитей, действующие на каждое из тел.
Так как грузы скользят без трения по плоскостям, силы реакции нитей направлены противоположно силам тяжести для каждого тела.
Для первого тела: R1 = m1 * g
Для третьего тела: R3 = (m3 + m4 + m5) * g
Для четвертого тела: R4 = (m4 + m5) * g
Для пятого тела: R5 = m5 * g
(где g - ускорение свободного падения)
Шаг 2: Найдем силу, действующую на блок 3.
Для этого надо учесть силу сопротивления M и силу F.
ΣF = F - M = ma (второй закон Ньютона)
Шаг 3: Найдем ускорение блока 3.
С учетом сил, действующих на блок 3, можем написать уравнение:
F - M = (m3 + m4 + m5) * a
Шаг 4: Найдем момент инерции блока 3.
I3 = 2 * (1/2 * m3 * (R^2 + r3^2) + m4 * (R^2 + r3^2) + m5 * (R^2 + r3^2)) = (m3 + m4 + m5) * (R^2 + r3^2)
Шаг 5: Найдем угловое ускорение блока 3.
ΣM = I * α
M * R3 - M * r3 = I3 * α
M * R - M * 0.5R = (m3 + m4 + m5) * (R^2 + r3^2) * α
M * 0.5R = (m3 + m4 + m5) * (R^2 + r3^2) * α
α = M * 0.5R / ((m3 + m4 + m5) * (R^2 + r3^2))
Шаг 6: Найдем угловую скорость блока 3.
ω = ω0 + α * t
где ω0 - начальная угловая скорость (равна 0, так как система изначально в покое), а t - время.
Шаг 7: Подставим значения и рассчитаем искомую величину.
m1 = 2 кг, m2 = 0, m3 = 4 кг, m4 = 0 кг (тело не входит в систему), m5 = 3 кг
M = 8 Н·м, F = 200 Н, угол φ = 60°, R = 0.5 м.
α = 8 Н·м * 0.5 м / ((4 кг + 0 кг + 3 кг) * (0.5 м^2 + (0.5 * 0.5 м)^2)) ≈ 10 рад/с^2 (округленно)
В нашем случае, угловая скорость будет вращения блока 3, поскольку он является частью механической системы.
ω = 0 + 10 рад/с^2 * t
Теперь мы можем рассчитать угловую скорость блока 3 в момент времени, когда он повернется на угол φ = 60°.
Угловая скорость будет равна:
ω = 10 рад/с^2 * t = φ / t
10 рад/с^2 * t = 60° / (π/180) рад
t ≈ (60° * 180/π рад) / 10 рад/с^2 ≈ 343,38 секунды (округленно)
Таким образом, угловая скорость блока 3 в момент времени, когда он повернется на угол φ = 60°, составляет приблизительно 343,38 секунды.