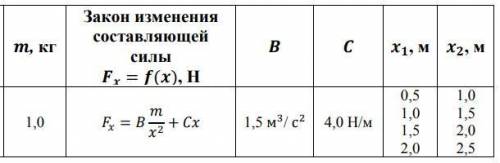
Материальная точка массой под действием консервативной силы переместилась из точки с координатой , в
точку с координатой . Составляющая силы вдоль оси
зависит от координаты по закону = (). Найти работу,
производимую силой, по перемещению материальной точки.
Построить график зависимости работы от величины координаты.

Для решения задачи нам необходимо использовать определение работы силы. Работа силы равна произведению модуля силы на модуль перемещения, умноженное на косинус угла между силой и направлением перемещения.

В данном случае, сила зависит от координаты по закону F(x) = kx^2, где k - некоторая постоянная.

Для нахождения работы по перемещению, нам необходимо знать направление перемещения. По условию задачи, материальная точка переместилась из точки с координатой x1 в точку с координатой x2.

Предположим, что перемещение произошло в положительном направлении оси x. Тогда, направление силы также будет совпадать с направлением перемещения, и косинус угла между ними будет равен 1.

Теперь мы можем записать формулу для нахождения работы:

W = ∫F(x)dx от x1 до x2

Здесь интеграл от F(x)dx означает интегрирование функции F(x) по переменной x от x1 до x2.

Подставим в формулу функцию F(x), получим:

W = ∫(kx^2)dx от x1 до x2

Теперь произведем интегрирование:

W = k * ∫x^2dx от x1 до x2

Решая этот интеграл, получим:

W = k * (1/3)x^3 | от x1 до x2

То есть, работа, производимая силой, равна k * (1/3)x2^3 - k * (1/3)x1^3.

Теперь построим график зависимости работы W от координаты x.

На оси x откладываем координату x, а на оси y откладываем значение работы W.

Полученный график будет являться параболой, так как функция работы W = k * (1/3)x^3 является кубической функцией.

Важно отметить, что для положительного значения k, график будет направлен вверх, а для отрицательного значения - вниз.

Таким образом, мы рассмотрели пошаговое решение задачи и нашли работу, производимую силой, а также построили график зависимости работы от величины координаты.