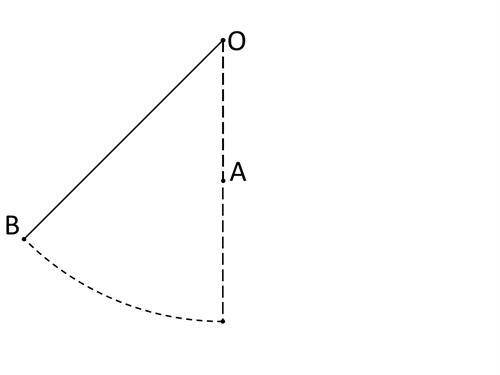
Математический маятник длиной 85 см совершает колебания параллельно вертикальной стенке. Ниже подвеса на расстоянии 21,25 см от точки подвеса (в точке А) в стенку забит тонкий гвоздь (смотри рисунок). Определи период колебаний такого маятника. При расчётах прими π=3,14, g=9,8 м/с².
(ответ округли до сотых.)
Другие вопросы по теме Физика
Популярные вопросы
- Проверьте являются ли тождественно равными выражения: 1. (а - 3) * (а +...
3 - Решите задание по алгебре 8 класс...
1 - Конспект на тему «Красные действовали на благо всего мира с идеей мировой...
3 - Командно-репрессивные методы управления легли в основу формирования авторитарной...
1 - ХЕЛП Зобразіть схематично графік функції ПОЛНОЕ РЕШЕНИЕ а) б) В)...
1 - Октябрь пришел к власти в России в результате социалистической революции...
3 - 584748585-747587+3668*5ставлю...
1 - можете написать тока ответ...
3 - 2. Какая информация соответствует тексту? Укажите несколько вариантов. А)...
2 - Сегодня в русский язык хлынул поток иностранных слов. Это ничего, это уже...
2
Период колебаний математического маятника можно выразить через его длину. В данном случае длина маятника равна 85 см. Формула для периода колебаний математического маятника выглядит следующим образом:
T = 2π√(L/g),
где T - период колебаний, L - длина маятника и g - ускорение свободного падения.
У нас уже указано значение ускорения свободного падения: g = 9,8 м/с², а длина маятника: L = 85 см = 0,85 м.
Подставим данные в формулу и решим уравнение:
T = 2π√(0,85/9,8).
Теперь посчитаем значение внутри корня:
√(0,85/9,8) ≈ 0,294.
Теперь подставим это значение обратно в формулу для периода колебаний:
T = 2π * 0,294 ≈ 1,85.
Ответ: период колебаний математического маятника составляет примерно 1,85 секунды (округляем до сотых).
Важно заметить, что в задаче не указано, что маятник малые колебания, поэтому мы используем общую формулу для периода колебаний. Если бы маятник совершал малые колебания, то период можно было бы определить как:
Т = 2π√(L/g).
Однако, в данном случае необходимо использовать полную формулу и указать, что маятник совершает колебания параллельно стенке.