Математический маятник длиной 1 м подвешен в вагоне, движущемся горизонтально с ускорением 4,2 м/с². Определи период колебаний такого маятника

Ответы

margo7108 15.10.2020 07:15

ответ: 1.9 с

Объяснение:

В том случае если бы маятник находился в вагоне поезда движущегося равномерно и прямолинейно или находящегося в состоянии покоя относительно выбранной ИСО, то период его колебаний можно было бы вычислить как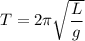 $T=2\pi \sqrt{\dfrac{L}{g}}$ , но так как по условию данной задачи поезд движется с ускорением, тем самым не являясь ИСО, то период колебаний маятника будет находиться иначе: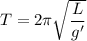 $T=2\pi \sqrt{\dfrac{L}{g'} }$

Где g' - результирующее ускорений a и g

Из рисунка видно что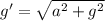 $g'=\sqrt{a^{2}+g^{2} }$ , тогда

$T=2\pi \sqrt{\dfrac{L}{\sqrt{a^{2}+g^{2} }} }$

$T=2\pi \sqrt{\dfrac{1}{\sqrt{4,2^{2}+9.8^{2} }} }\approx 1,9$ с

Математический маятник длиной 1 м подвешен в вагоне, движущемся горизонтально с ускорением 4,2 м/с².

ПОКАЗАТЬ ОТВЕТЫ

NorthIndiana 13.01.2024 16:09

Хорошо, давай разберемся с этим вопросом.

Период колебаний математического маятника определяется формулой:
T = 2π√(L/g),

где T - период колебаний,
L - длина маятника,
g - ускорение свободного падения.

В данной задаче длина маятника равна 1 м, а ускорение свободного падения принимается за 9,8 м/с² (данное значение обычно используется в физических задачах, так как свободное падение относится к земному гравитационному полю).

Но в данном случае вагон движется горизонтально с ускорением 4,2 м/с². Поэтому, чтобы определить период колебаний маятника, нужно использовать подходящее ускорение.

Вертикальное ускорение маятника, вызванное ускорением вагона, равно -a*cos(θ), где a - ускорение вагона, θ - угол отклонения маятника от вертикали.

Так как у нас вертикальный маятник, то θ = 0, и угол отклонения равен нулю. То есть, вертикальное ускорение маятника равно -a.

Тогда, ускорение свободного падения g' внутри вагона будет равно g + a (ускорение свободного падения плюс ускорение движения вагона):
g' = g + a,
g' = 9,8 м/с² + 4,2 м/с²,
g' = 14 м/с².

Теперь мы можем вставить это значение в формулу периода колебаний:
T = 2π√(L/g').

T = 2π√(1 м/14 м/с²).

Выполним вычисления:

T = 2π * √(1/14).
T = 2π * (√1/√14).
T = 2π * (1/√14).
T = 2π/√14.

Теперь можем рассчитать приближенное значение периода колебаний маятника:

T ≈ (3.1416 * 2)/√14.
T ≈ 6.2832/√14.
T ≈ 6.2832/3.7417.
T ≈ 1.6779 с.

Таким образом, период колебаний такого математического маятника, подвешенного в вагоне, движущемся горизонтально с ускорением 4,2 м/с², составляет приблизительно 1,6779 секунды.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Физика