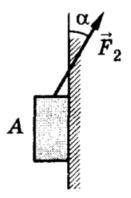
Магнит A массой m = 5кг кг притягивается к стенке с силой F1 = 5H. Если к магниту приложить ещё силу F2 = 20H (рис.), составляющую угол alpha = 30° со стенкой, то куда и с каким ускорением будет двигаться магнит? Коэффициент трения между стенкой и магнитом mu = 0,2. При каких значениях mu магнит не будет двигаться?

Для того чтобы ответить на этот вопрос, нам нужно разобраться с силами, действующими на магнит.

Первая сила, действующая на магнит, - это сила притяжения со стороны стены, обозначенная как F1. Она равна 5H и направлена влево.

Вторая сила, действующая на магнит, - это сила, приложенная к нему, обозначенная как F2. Она равна 20H и образует угол 30° со стеной.

Теперь мы можем разложить силу F2 на две составляющие - горизонтальную и вертикальную. Горизонтальная составляющая силы F2 равна F2*cos(alpha), а вертикальная составляющая равна F2*sin(alpha).

Таким образом, горизонтальная составляющая силы F2 будет направлена вправо и равна 20H*cos(30°), а вертикальная составляющая будет направлена вниз и равна 20H*sin(30°).

Теперь мы можем рассмотреть силу трения, действующую между магнитом и стенкой. Согласно заданию, коэффициент трения между стенкой и магнитом равен 0,2.

Сила трения Fтрения равна mu*m*g, где mu - коэффициент трения, m - масса магнита и g - ускорение свободного падения, примерно равное 9,8 м/с^2.

Теперь мы можем приступить к решению задачи.

1. Рассмотрим горизонтальные силы, действующие на магнит: сила притяжения F1 и горизонтальная составляющая силы F2. Так как F1 направлена влево, а горизонтальная составляющая силы F2 направлена вправо, то мы можем разность этих сил на равновесие между ними: F1 - F2*cos(30°) = 5H - 20H*cos(30°). Подставляя числовые значения, получаем: 5H - 20H*cos(30°) = 5H - 20H*sqrt(3)/2 = 5H - 10H*sqrt(3).

2. Теперь рассмотрим вертикальные силы, действующие на магнит: вертикальная составляющая силы F2 и сила трения Fтрения. Так как вертикальная составляющая силы F2 направлена вниз, а сила трения Fтрения направлена вверх, то мы можем суммировать эти силы на равновесие между ними: F2*sin(30°) - Fтрения = 20H*sin(30°) - mu*m*g. Подставляя числовые значения, получаем: 20H*sin(30°) - mu*m*g = 20H*0,5 - 0,2*5кг*9,8 м/с^2.

3. Так как магнит двигается только горизонтально, нам нужно найти значение F1 - F2*cos(30°), при котором магнит будет находиться в равновесии. Если это значение равно 0, то магнит не будет двигаться.

4. Так же нам нужно найти значение 20H*sin(30°) - mu*m*g, при котором магнит будет находиться в равновесии. Если это значение меньше или равно 0, то магнит не будет двигаться.

Таким образом, чтобы ответить на последние два вопроса, нам нужно решить уравнения из пунктов 3 и 4 и сравнить результаты с 0. Если значение равно 0 или меньше, то магнит не будет двигаться. Если больше 0, то магнит будет двигаться в заданном направлении.