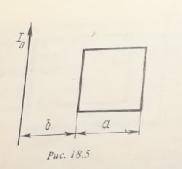
Квадратная проволочная рамка со стороной а и длинный прямой провод с током I0 лежат в одной плоскости, как показано на рис. 18.5. Расстояние от провода до ближайшей к нему стороны рамки b. Сопротивление рамки R. Определить ток I0, если известно, что при его выключении в рамке проходит электрический заряд q. Самоиндукцией контура пренебречь.

Для решения задачи нам понадобятся законы электромагнетизма, а именно закон Ампера и закон Ома.

Закон Ампера гласит, что интеграл от магнитного поля B по замкнутому контуру равен произведению ампер-витв на электрический ток, пронизывающий этот контур:
∮B·dl = μ0·I,
где B - магнитное поле, dl - элемент длины контура, μ0 - магнитная постоянная, I - ток.

Закон Ома говорит о том, что напряжение U на элементе цепи равно произведению сопротивления R на силу тока I:
U = I·R.

Согласно условию задачи, при выключении тока I0 в рамке проходит электрический заряд q. Так как самоиндукцией контура можно пренебречь, то изменение потока магнитного поля в рамке при выключении тока равно -L·ΔI, где L - коэффициент самоиндукции, ΔI - изменение тока.

Заметим, что поток магнитного поля, пронизывающего рамку, при выключении тока равен разности потоков от прямого провода и от двух боковых проводов рамки, так как поток от верхнего и нижнего проводов рамки равен 0, поскольку он проходит по рамке параллельно их направлению.

Поток от прямого провода равен:
Φпрям.пров. = B·L1,
где L1 - длина прямого провода, B - магнитная индукция.

Поток от двух боковых проводов рамки равен:
Φбок.пров. = 2·B·L2,
где L2 - длина боковых проводов рамки.

Таким образом, изменение потока магнитного поля равно:
ΔΦ = Φпрям.пров. + Φбок.пров. = B·L1 + 2·B·L2 = B·(L1 + 2·L2).

С другой стороны, изменение потока магнитного поля равно -L·ΔI, поэтому:
-L·ΔI = B·(L1 + 2·L2).

Преобразуем это уравнение, выразив ΔI через I0 и I:
ΔI = I - I0.

Подставляем выражение для ΔI в уравнение:
-L·(I - I0) = B·(L1 + 2·L2).

Откуда получаем:
L·I - L·I0 = B·(L1 + 2·L2).

Выразим B через I0, R и a:
B = μ0·I0/(2π·a).

Подставляем выражение для B в уравнение:
L·I - L·I0 = μ0·I0/(2π·a)·(L1 + 2·L2).

Преобразуем это уравнение, выразив I через I0:
I = (μ0·I0/(2π·a)·(L1 + 2·L2) + L·I0)/L.

Таким образом, ток I0 можно определить, зная параметры рамки (a, L1, L2) и значения электрического заряда q, который проходит через рамку при выключении тока I0. Подставив эти значения в полученное уравнение, можно найти искомый ток I0.