1. Физика
  2. Космический корабль массой

Космический корабль массой покоя m=20т летит со скоростью v=0,25с. какова его кинетическая энергия? дайте решение ответ: 5,9*10^19 дж.

S1mple11111 S1mple11111    1   01.07.2019 22:50    21

Ответы
Jirnyi Jirnyi  26.07.2020 08:59

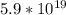ответ: 5.9*10^{19} Дж

Объяснение:

Дано:

m=20 т =20000 кг

v=0.25c

----------------------------------

E_{k} -?

Т.к. в условии задачи сказано, что скорость  v составляет 25% от скорости распространения электромагнитного излучения вакууме, то пользоваться классической механикой и считать что кинетическая энергия тела всегда равна половине произведения массы покоя тела на квадрат его скорости мы не будем, а перейдем на СТО и ЗСЭ

Согласно ЗСЭ  

E=E_{k} +E_{0}

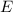Где E - полная энергия тела; Согласно СТО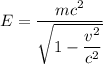  E=\dfrac{mc^{2} }{\sqrt{1-\dfrac{v^{2} }{c^{2} } } }

E_{k} - кинетическая энергия тела

E_{0} - энергия покоя тела; E_{0}= mc^{2

m - масса покоя тела

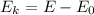
Отсюда E_{k} = E -E_{0}

E_{k} = \dfrac{mc^{2} }{\sqrt{1-\dfrac{v^{2} }{c^{2} } } } -mc^{2} ⇒ E_{k} = mc^{2}(\dfrac{1 }{\sqrt{1-\dfrac{v^{2} }{c^{2} } } } -1)

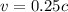
При v=0.25c

E_{k} = mc^{2}(\dfrac{1 }{\sqrt{1-\dfrac{0.25^{2} c^{2} }{c^{2} } } } -1) ⇒ E_{k} = mc^{2}(\dfrac{1 }{\sqrt{0.9375 } } } -1)

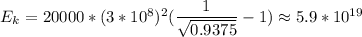Поэтому E_{k} = 20000*(3*10^{8}) ^{2}(\dfrac{1 }{\sqrt{0.9375 } } } -1) \approx 5.9*10^{19} Дж

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
NasFan NasFan  01.09.2020 13:26
Физикалық теориялар қалай жасалады​...
Коте0под0наркоте Коте0под0наркоте  01.09.2020 13:28
Укажите верный или неверный стихотворение родной очаг​...
Агентс Агентс  02.09.2020 13:26
-20°C :125°C температура мандерин келвинге ауыстыру т​...
ovosh228322 ovosh228322  01.09.2020 13:16
Шелекті құдық түбінен арқанмен көтеріп шығару үшін 250 Дж жұмыс атқару қажет. Осы шелекті шығыр көмегімен көтерген кездегі атқарылған жұмысты табыңыз физика​...
brainsofi1 brainsofi1  01.09.2020 13:47
Жүзгіш өзеннің ағысымен жүзіп келеді . Егер өзен ағысының жылдамдығы 0,5 м / с және жүзгіштің суға салыстырғандағы жылдамдығы 2 м / с болса , онда жүзгіштің жағамен салыстырған...
bondiserj bondiserj  01.09.2020 13:49
Шынайы омирдеги броундык козгалыс теориясы жайлы хабарлама жазу​...
лолололололпке лолололололпке  01.09.2020 13:50
Опираясь на рисунок 1.2 объясните характер движения броуновской частицыможно кРатко и...
Mrskiss Mrskiss  31.07.2019 06:00
1) на заряд 15 мккл в некоторой точке электрического поля действует сила 0,01 н. определите напряженность электрического поля в этой точке? 2) найти напряженность электрического...
yanademchenko38 yanademchenko38  31.07.2019 06:00
Решить если можно напишите подробно на листочке от руки , и выложите фото . по какую работу совершит сила при удлинении пружины жесткостью 350 н/м от 4 см до 6 см? 1) 0,07...
banilchik26 banilchik26  31.07.2019 06:10
Сколько электронов проходит через поперечное сичение проводника за 2нс при силе тока 24 мка...

Популярные вопросы