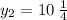Камень бросили вертикально вверх с начальной скоростью 15 м/с от поверхности земли.На каком расстояний от поверхности земли потенциальная энергия камня уменьшится в 9 раз?
Другие вопросы по теме Физика
Популярные вопросы
- Посчитайте,сколько число а встречается в строке...
2 - Task. Rewrite the sentences in the passive. My brother lent me...
2 - Women: Elephants or Hummingbirds? Sir, I am writing in answer to...
2 - Рационал санды шексіз периодты ондық бөлшек түрінде беру. Шексіз...
2 - на расстоянии 2-3 м от своих одноклассников Распределите в течение...
1 - Яка тема і ідея роману у віршах Пушкіна Євгенія Онєгіна...
1 - 3. Специалисты изготовили наградной кубок массой 3 кг, выполненный...
3 - Определите, к какой разновидности научного стиля они относятся,...
3 - Узнайте о влиянии льда на жизнь людей и экономику. Опишите положительное...
3 - Евгеній Онєгін 3-4 глава сюжетний ланцюг ...
2
Дано:
Найти: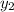
По условию , тогда можем найти
, тогда можем найти 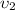 :
:
Мы нашли скорость в тот момент времени, когда кинетическая энергия стала в девять раз меньше. Таким образом, зная эту скорость, начальную скорость и ускорение (которое равно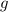 ), мы можем найти время, за которое камень долетел до этой точки.
), мы можем найти время, за которое камень долетел до этой точки.
Т.е. камень двигался до этой точки 1 секунду. Напишем уравнение координаты для равноускоренного движения:
Нам нужно найти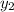 , подставим в формулу все найденные значения.
, подставим в формулу все найденные значения.
ответ: