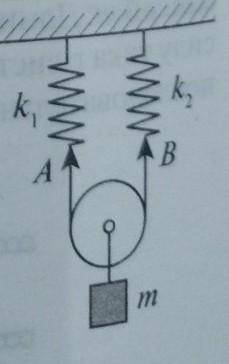
К оси подвижного лёгкого блока, подвешенного на невесомой нерастяжимой нити AB, соединённой с двумя пружинами жёсткостью k1=10 H/м и k2=20 H/м, прикреплено тело m=100г, так как показано на рисунке. Блок может свободно скользить по нити. Пренебрегая трением в оси блока, определите период малых колебаний тела
Другие вопросы по теме Физика
Популярные вопросы
- прям сейчас створити гроно-характеристику образу Міо(Бу Вільгельма Ульсона)...
1 - Доможіть будь ласка з історії України! Поміркуйте, чи можна було уникнути...
3 - Знайдіть помилкове твердження. А.) Тихий океан з’єднується з Індійським...
3 - 1. Какие преобразования Столыпин считал необходимыми для страны?2. Какие...
1 - Встреча с Родиной – это праздник. С. Бабенко «Тюе-Тас» Чувства автора...
1 - Какие реформы провел Отто фон Бисмарк и описания этих реформ...
2 - Привет! Сейчас лежу, греюсь под ярким и нежным Мексиканским солнышкомвозле...
3 - Зделать там не сложно но мне не хватает времени...
3 - Нужно построить изображение в линзе и дать характеристику ...
1 - Сочинение на тему Утро в сосновом бору 1)про автора (его биография )2)про...
3
1. Закон Гука для первой пружины:
F1 = -k1x, где F1 - сила, k1 - жёсткость пружины, x - смещение от положения равновесия.
2. Закон Гука для второй пружины:
F2 = -k2x, где F2 - сила, k2 - жёсткость пружины, x - смещение от положения равновесия.
3. Сила натяжения нити:
F3 = T, где T - натяжение нити.
4. Учитывая, что система находится в положении равновесия, сумма всех сил равна нулю:
F1 + F2 + F3 = 0.
Подставим значения сил из закона Гука:
-k1x - k2x + T = 0.
5. Найдём суммарную жёсткость системы:
k = k1 + k2.
6. Подставим значение T из уравнения в пункте 4:
-k1x - k2x + (k1 + k2)x = 0.
7. Упростим выражение:
(-k1 - k2 + k1 + k2)x = 0,
0x = 0.
Следовательно, получаем, что при любом x сумма всех сил равна нулю, что соответствует положению равновесия.
8. Теперь найдём период колебаний системы.
Период колебаний связан со суммарной жёсткостью системы и массой малого тела m следующим образом:
T = 2π√(m / k).
Подставим значения m и k:
T = 2π√(0.1 / (10 + 20)).
9. Упростим выражение:
T = 2π√(0.1 / 30),
T = 2π√(1 / 300).
10. Имея величину выражения, можно приближённо рассчитать значение периода колебаний системы, с помощью калькулятора или компьютерной программы.
Таким образом, период малых колебаний тела в данной системе будет приближённо равен 0.2563 секунды (при округлении до 4 знака после запятой).