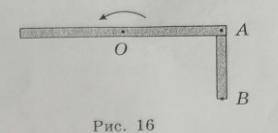
Изогнутая палочка (рис. 16) вращается с постоянной скоростью, равной 10 рад/с, относительно оси, проходящей через точку О. Длина всей палочки равна 80 см, а части АВ — 30 см. Определите линейные скорости υΑ и υΒ точек А и В.
Другие вопросы по теме Физика
Популярные вопросы
- Вычислить значение выражений: a) 36 div 4 б) 77 mod 2 в) 78 div 300 г)...
1 - Назовите отличие выделительной системы у рыб и собаки...
2 - Запишите выражения,используя символы...
3 - відстань між 2 точками розрядами Q1=1мкк Q2=-0.1мкк відстань між ними...
2 - Задание Прочитайте тексты и выполните задания.Более 45 лет назад в 50...
1 - 1. Прочитайте текст. 2. Выделите микротемы в тексте. 3. Выберите цитаты,...
1 - Железобетонная плита, длиной 350 см и шириной 150 см, полностью погружена...
1 - Найди три верных утверждения Всемирная история...
1 - Найдите величину угла AOD, если О - центр правильного двенадцатиугольника...
3 - Распишите: 1) Какое место занимали данные социальные группы в обществе. ...
2
Линейная скорость точки А (υΑ) будет складываться из двух компонент: скорости точки В (υΒ) и скорости точки О (υО).
Для начала определим скорость точки О (υО). Так как палочка вращается вокруг оси О, скорость точки О будет нулевой. Это означает, что линейная скорость точки О (υО) равна 0 см/с.
Теперь рассмотрим точку В. Поскольку палочка вращается с постоянной скоростью 10 рад/с, скорость точки В будет зависеть от радиуса вращения. Длина всей палочки равна 80 см, а часть АВ равна 30 см. Таким образом, радиус вращения точки В будет 80 см - 30 см = 50 см.
Для вычисления линейной скорости точки В (υΒ) воспользуемся формулой вращения:
υ = ω * r
где ω - угловая скорость, а r - радиус вращения.
Подставляем известные значения:
υΒ = 10 рад/с * 50 см = 500 см/с
Таким образом, линейная скорость точки В (υΒ) равна 500 см/с.
Наконец, чтобы найти линейную скорость точки А (υΑ), складываем линейную скорость точки В (υΒ) и линейную скорость точки О (υО):
υΑ = 500 см/с + 0 см/с = 500 см/с
Таким образом, линейная скорость точки А (υΑ) равна 500 см/с.
Итак, линейные скорости точек А и В равны 500 см/с.