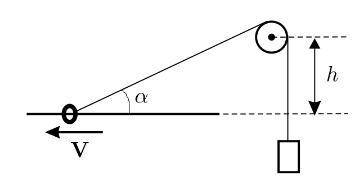
Груз связан с кольцом идеальной нитью, переброшенной через блок. Кольцо скользит с постоянной скоростью V по горизонтальной спице, расположенной на h ниже блока (см. рис.). Найти ускорение груза в момент, когда угол между наклонной частью нити и спицей равен α.
Другие вопросы по теме Физика
Популярные вопросы
- Вычислите площадь круга,радиус которого равен 2дм (пи=3,1)...
1 - Жители населённых пунктов единственного и множественного числа на суффикс ец...
3 - Как называется птица с крыльями в 1 метр и окрасом чисто серым, похожа на...
1 - Каких результатов удалось добиться князю олегу в войне с хазарами...
2 - Трамвай за 2\3 часов проезжает расстояние 10 1\6 км найдите скорость трамвая...
1 - Рассматривая иллюстрации в книгах, снеговик увидел… себя. только необычного....
1 - Напишите сочинение рассуждение на тему какой школьный предмет вам больше всего...
1 - Какие виды искусства объединяет в себе спектакль?...
1 - Вчем с точки зрения отца гринева состоит долг дворянина? капитанская дочка,...
3 - Найдите координаты вектора a1 a2 если точки a1,a2 имеют координаты (-3; 5), (2;...
1
Объяснение:
Очевидно, что нить и груз движутся со скоростью, равной проекции скорости кольца на эту нить
Тогда, через малый промежуток времени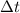
Раскроем косинус разности, учитывая что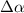 малое
малое
Изменение скорости нити
Теперь свяжем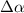 и
и 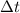 , проще всего это сделать, рассмотрев
, проще всего это сделать, рассмотрев 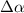 как центральный угол некоторой малой дуги окружности с радиусом, равным первоначальной длине нити
как центральный угол некоторой малой дуги окружности с радиусом, равным первоначальной длине нити
Таким образом
Но ускорение, по определению, есть отношение малых изменений скорости и времени