Груз, подвешенный на длинном резиновом жгуте, совершает колебания с периодом Т. Как изменится частота колебаний, если отрезать 1/2 длины жгута?

Возрастет в √2 раз

Объяснение:

Давайте посмотрим как зависит коэффициент жесткости жгута от его длины. Запишем закон Гука:

где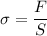 - нормальное напряжение, Е - модуль Юнга, 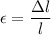-относительное удлинение жгута, таким образом:

Разделим обе части выражения на Δl, учитывая что F/Δl=k:

Значит, коэффициент жесткости жгута обратно пропорционален его длине и при укорочении жгута в 2 раза коэффициент жесткости увеличится в два раза. Согласно формуле для периода колебаний пружинного маятника:

Частота колебаний:

Как видим, частота колебаний должна возрасти в √2 раз.