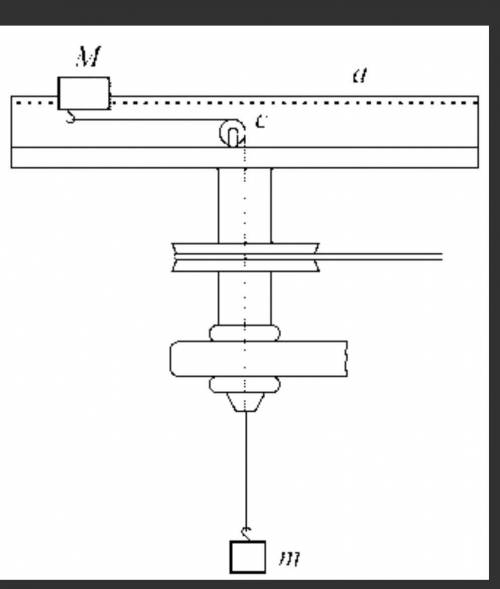
Груз массы М может скользить без трения по стержню а, укрепленному перпендикулярно к оси вращающейся центробежной машины. Ось машины вертикальна, и сквозь нее проходит нить, на которой висит груз массы m; нить перекинута через блок с и другой ее конец прикреплен к грузу массы М. Найти положение груза массы М на стержне а, когда центробежная машина вращается с угловой скоростью ω.
Другие вопросы по теме Физика
Популярные вопросы
- Паразиттерге қандай жануарлар жатады...
2 - 2.5. Торкөз қағазға 2.7-суретте көрсетілгендей етіп CE сәулесі...
3 - Агылшын протесттарының жалпы атауы кандай?...
2 - Русский язык седьмой класс 16 упражнение Б ,16 страница...
1 - По рисункам объясните значимость полевого метода иисследования.Я...
1 - Rewrite each sentence in two ways, using the underlined words as...
2 - Пліз напишіть хотяби одну як шо годні то дві...
1 - 1. Төмендегі кестені пайдаланып, оқыған үзіндідегі кейіпкерлерге...
1 - Выписать из любого текста художественной литературы 5 предложений...
3 - 1. 1) х = 11 және у = 88; 2) x = 144 және у12;3) х = 53 және у...
2
Момент импульса груза массы М относительно оси вращения равен моменту импульса груза массы m, висящего на нити.
Момент импульса груза массы М:
L1 = М * v1
Момент импульса груза массы m:
L2 = m * v2 * L
где v1 - скорость скольжения груза М, v2 - скорость груза m на окружности радиусом L.
Так как груз М скользит по стержню без трения, его скорость равна нулю:
v1 = 0
Также, груз m вращается по окружности радиусом L, и его скорость связана с угловой скоростью вращения ω и радиусом L следующим образом:
v2 = ωL
Теперь можем записать уравнение моментов импульса:
L1 = L2
М * v1 = m * v2 * L
0 = m * (ωL)^2 * L
Для упрощения уравнения, можно заменить (ωL)^2 на g, где g - ускорение свободного падения:
0 = m * g * L^2
Таким образом, мы получаем, что положение груза массы М на стержне а, когда центробежная машина вращается с угловой скоростью ω, определяется равенством:
m * g * L^2 = 0
Очевидно, что L не может быть равен нулю, так как это противоречит самой постановке задачи. Таким образом, получаем, что:
m * g = 0
Отсюда следует, что груз массы М не имеет определенного положения на стержне а и может находиться в любом месте.