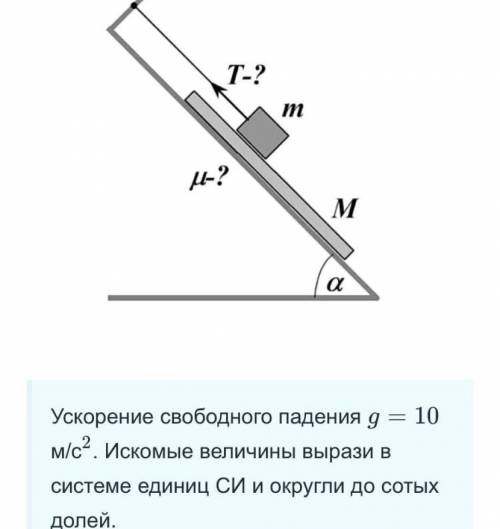
Гладкий кубик массой m = 1 кг Находится на доске массой M = 3 кг, покоящейся на наклонной плоскости с углом наклона a = 45°, и удерживается в равновесии нитью, как показано на рисунке. Удерживающая нить параллельна наклонной плоскости. Найди 1) силу натяжения нити T; 2) при каком минимальном значении коэффициента трения q между доской и наклонной плоскостью равновесие доски возможно. Трением кубика о доску пренебречь.

Для решения данной задачи, мы можем использовать законы Ньютона и принципы равновесия. 1) Для определения силы натяжения нити (T) мы должны рассмотреть свободное тело – доску. Силы, действующие на доску: - Сила тяжести доски (Fg_doska), которая направлена вниз и равна произведению массы доски (M) на ускорение свободного падения (g): Fg_doska = M * g. - Сила наклона доски (Fn_doska), которая действует перпендикулярно наклонной плоскости и направлена в противоположную сторону силы тяжести. - Вертикальная составляющая силы натяжения нити (T_vert), которая действует вверх и равна Fg_doska + Fn_doska. Так как доска находится в равновесии, то сумма всех сил, действующих на неё, должна быть равна нулю. Тогда мы можем записать уравнение равновесия по вертикальной оси: T_vert - Fg_doska - Fn_doska = 0. Учитывая, что сила наклона доски равна произведению массы кубика (m) на ускорение свободного падения (g): Fn_doska = m * g, мы можем переписать уравнение равновесия в следующем виде: T_vert - Fg_doska - m * g = 0. Подставляя значения Fg_doska = M * g и Fn_doska = m * g, мы получаем уравнение: T_vert - M * g - m * g = 0. Теперь мы можем выразить вертикальную составляющую силы натяжения нити (T_vert): T_vert = (M + m) * g. Учитывая, что нить параллельна наклонной плоскости, вертикальная составляющая силы натяжения нити также равно вертикальной силе тяжести кубика: T_vert = Fg_kubika = m * g. Таким образом, мы можем записать выражение для силы натяжения нити (T): T = m * g. 2) Для определения минимального значения коэффициента трения (q) между доской и наклонной плоскостью, при котором равновесие доски возможно, мы должны рассмотреть горизонтальные составляющие сил. Силы, действующие по горизонтали на доску: - Горизонтальная составляющая силы натяжения нити (T_horiz), которая направлена вдоль наклонной плоскости. - Сила трения (Ftr), которая действует в противоположную сторону движения доски. Так как доска находится в равновесии, то сумма всех горизонтальных сил, действующих на неё, должна быть равна нулю. Тогда мы можем записать уравнение равновесия по горизонтали: T_horiz - Ftr = 0. Силу трения (Ftr) можно выразить через коэффициент трения (q) и нормальную реакцию (Fn_doska): Ftr = q * Fn_doska. Сила наклона доски (Fn_doska) равна произведению массы кубика (m) на ускорение свободного падения (g): Fn_doska = m * g. Таким образом, мы получаем уравнение: T_horiz - q * m * g = 0. Мы знаем, что горизонтальная составляющая силы натяжения нити (T_horiz) равна силе трения (Ftr): T_horiz = Ftr = q * m * g. Теперь мы можем записать выражение для коэффициента трения (q): q = T_horiz / (m * g). Таким образом, минимальное значение коэффициента трения (q), при котором равновесие доски возможно, будет равно: q = T_horiz / (m * g).