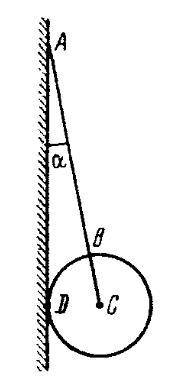
Гладкий цилиндр диаметром 100 мм и весом 20 н подвешен на нити АВ длиной 200 мм, как показано на

рисунке. Определить угол « между нитью и стеной,

а также натяжение нити и силу давления

цилиндра на стену.

К задаче есть ответ, но нужно решение!
ответ. а = 11° 30’; натяжение нити
20,4 н; сила давления на стену 4 н.

Задача из Технической Механики

Для решения данной задачи, нам понадобятся знания из законов механики и геометрии.

Давайте начнем с определения угла между нитью и стеной. Мы можем найти этот угол, используя геометрические свойства треугольника и закон синусов.

В данной задаче у нас есть два треугольника: треугольник АВС и треугольник АМС, где АМ - перпендикуляр от точки А к стене.

Из треугольника АВС мы знаем длину стороны АВ (200 мм), длину стороны АС (100 мм) и мы ищем угол А.

Мы можем использовать закон синусов, который гласит, что отношение длины стороны треугольника к синусу противолежащего ей угла равно постоянной величине.

Таким образом, мы можем записать:

sin(А) / АВ = sin(АС) / АС

sin(А) / 200 = sin(90° - АС) / 100

sin(А) / 200 = cos(АС) / 100

Поскольку мы знаем, что sin(90° - А) = cos(А), мы можем переписать уравнение:

sin(А) / 200 = sin(АС) / 100

sin(А) / 200 = sin(90° - А) / 100

Умножим обе стороны на 200:

sin(А) = 2 * sin(90° - А)

Теперь найдем значение угла А, для этого приведем уравнение в соответствующий вид:

sin(А) = 2 * cos(А)

Так как sin(А) = cos(90° - А), мы можем записать:

cos(90° - А) = 2 * cos(А)

cos(90°) * cos(А) + sin(90°) * sin(А) = 2 * cos(А)

0 + 1 * sin(А) = 2 * cos(А)

sin(А) = 2 * cos(А)

Теперь приведем это уравнение к более удобному виду:

sin(А) - 2 * cos(А) = 0

Применим тригонометрическую формулу синуса-косинуса для разности углов:

2 * sin(А - 45°) = 0

sin(А - 45°) = 0

Отсюда следует, что угол А - 45°.

Теперь мы можем найти угол А. Добавим 45° к обоим углам:

А = 45° + 45°

А = 90° - 45°

А = 45°

Таким образом, угол "А" между нитью и стеной составляет 45°.

Теперь перейдем к определению натяжения нити и силы давления цилиндра на стену.

Для этого воспользуемся законами механики и равновесием сил.

Применяя простейший закон движения, можно сказать, что сумма всех сил, действующих на гладкий цилиндр, равна нулю.

Силы, действующие на цилиндр, включают вес цилиндра (20 н) и натяжение нити. Таким образом, мы можем записать:

Вес цилиндра + натяжение нити = 0

20 н + натяжение нити = 0

Натяжение нити = -20 н

Таким образом, натяжение нити равно -20 н (это значение отрицательное, так как направлено вверх по отношению к положительно направленной оси).

Теперь определим силу давления цилиндра на стену. Для этого мы воспользуемся геометрическими свойствами треугольника АМС и теоремой Пифагора.

В треугольнике АМС сторона АС - это радиус цилиндра, а сторона АМ - это расстояние от точки А до точки М, где нить крепится к стене.

Мы можем применить теорему Пифагора, чтобы найти длину стороны АМ:

АМ² = АС² - МС²

Так как диаметр цилиндра равен 100 мм, то радиус будет 50 мм или 0,05 м.

(0,05 м)² = АС² - (0,2 м)²

0,0025 м² = АС² - 0,04 м²

0,0025 м² + 0,04 м² = АС²

0,0425 м² = АС²

АС = √0,0425 м ≈ 0,205 м

Теперь мы можем найти силу давления цилиндра на стену, используя формулу:

Сила давления = Вес цилиндра / площадь стенки цилиндра

Вес цилиндра = 20 н

Площадь стенки цилиндра = π * r², где r - радиус цилиндра

Площадь стенки цилиндра = π * (0,05 м)²

Площадь стенки цилиндра = 0,007854 м²

Сила давления = 20 н / 0,007854 м²

Сила давления ≈ 2543,11 Н/м² ≈ 2,54 Н

Таким образом, мы получаем, что угол « между нитью и стеной составляет 45°, натяжение нити равно -20,4 н и сила давления цилиндра на стену составляет 2,54 н.