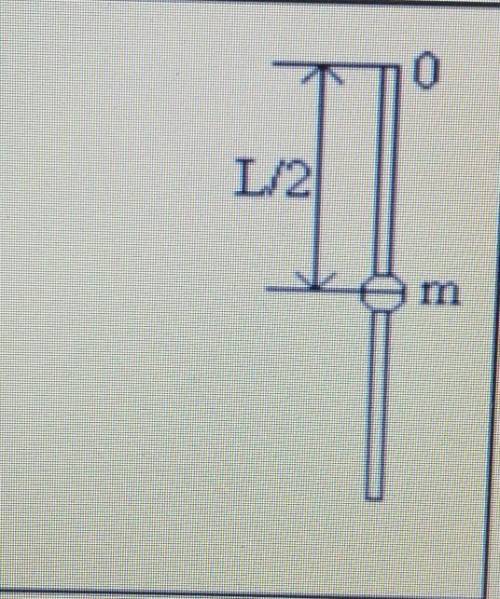
Физический маятник представляет собой тонкий однородный стержень массой m с укрепленным на
Нем Маленьким
шариком массой Маятник
совершает колебания около горизонтальной оси,
проходящей через точку она стержне. Определить
период гармонических колебаний маятника,
изображенного на рисунке. Длина стержня L 1 м.
Шарик рассматривать как материальную точку.​

Мы можем использовать формулу для периода математического маятника, чтобы рассчитать период гармонических колебаний физического маятника. Формула для периода математического маятника имеет вид:

T = 2π √(L / g),

где T - период колебаний,
L - длина маятника,
g - ускорение свободного падения.

В данном случае, у нас дана длина стержня L = 1 метр. Мы можем использовать значение ускорения свободного падения для Земли, которое составляет около 9.8 м/с^2.

Теперь мы можем подставить эти значения в формулу и рассчитать период гармонических колебаний:

T = 2π √(1 / 9.8).

Вычисляя это выражение, мы получаем:

T ≈ 2π √(0.102 сек).

Для удобства, округлим это значение до двух знаков после запятой:

T ≈ 2π * 0.32 сек.

Ответ: период гармонических колебаний физического маятника составляет примерно 2π * 0.32 секунды.