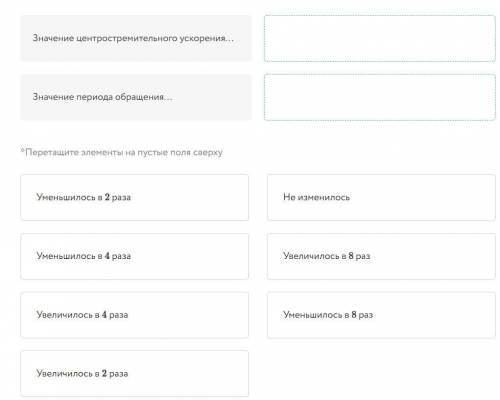
Движение по окружности Радиус движения тела по окружности и его линейную скорость увеличили в 2 раза. Как при этом изменились значения периода обращения тела по окружности и его центростремительного ускорения?

Добрый день! Давайте рассмотрим ваш вопрос.

Итак, у нас есть тело, движущееся по окружности. Радиус его движения и линейная скорость увеличены в 2 раза. Мы должны определить, как изменятся значения периода обращения тела по окружности и его центростремительного ускорения.

Период обращения тела по окружности (T) - это время, за которое тело делает один полный оборот по окружности.

Центростремительное ускорение (a) - это ускорение направленное в сторону центра окружности.

Чтобы решить эту задачу, нам нужно использовать известные формулы и законы движения по окружности.

1. Формула для периода обращения тела по окружности:
T = 2πr/v,

где r - радиус окружности, а v - линейная скорость тела.

Поскольку радиус движения тела увеличивается в 2 раза (r1 = 2r), а линейная скорость также увеличивается в 2 раза (v1 = 2v), то новый период обращения будет:

T1 = 2πr1/v1 = 2π(2r)/2v = 2πr/v = T.

Итак, значение периода обращения тела по окружности не изменится и останется таким же.

2. Формула для центростремительного ускорения:
a = v^2/r,

где v - линейная скорость тела, а r - радиус окружности.

Поскольку линейная скорость увеличивается в 2 раза (v1 = 2v), а радиус движения тела также увеличивается в 2 раза (r1 = 2r), то новое центростремительное ускорение будет:

a1 = v1^2/r1 = (2v)^2/(2r) = 4v^2/(2r) = 2v^2/r.

Итак, значение центростремительного ускорения также увеличивается в 2 раза.

Итак, чтобы ответить на ваш вопрос, при увеличении радиуса движения тела по окружности и его линейной скорости в 2 раза, значение периода обращения тела по окружности не изменится и останется таким же, а значение центростремительного ускорения увеличится в 2 раза.

Надеюсь, это помогло вам и ответ был понятен. Если у вас есть еще вопросы, не стесняйтесь задавать их!