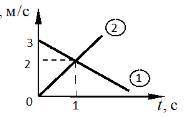
Две материальные точки 1 и 2 в момент времени t=0 выходят из точки с координатой x=0 и движутся в положительном направлении оси OX . Используя графики зависимости от времени t проекций Vx1 и Vx2 скоростей точек, найдите расстояние от места начала движения до места встречи.

Для решения задачи, нам нужно построить графики зависимости от времени t проекций Vx1 и Vx2 скоростей точек и найти момент времени, когда проекции скоростей точек становятся одинаковыми.

Исходя из графика зависимости от времени t проекции Vx1 скорости точки 1, мы видим, что вначале скорость растет медленно, а затем рост становится более быстрым. После определенного момента времени t1 скорость начинает убывать, исходя из уровня 0, до того как стать отрицательной. Это говорит нам, что точка 1 двигается в положительном направлении, затем замедляется и начинает двигаться в отрицательном направлении.

Из графика зависимости от времени t проекции Vx2 скорости точки 2, мы видим, что вначале скорость растет ровно и линейно, затем остается постоянной в течение некоторого времени после t2, и затем рост становится более быстрым. Это говорит нам, что точка 2 движется в положительном направлении, затем ускоряется и затем снова замедляется.

Теперь нам нужно найти момент времени, когда проекции скоростей точек становятся одинаковыми. По графикам, мы видим, что вначале скорость точки 2 ниже, чем скорость точки 1. Затем, после некоторого времени t1, скорость точки 1 начинает убывать, и скорость точки 2 становится выше.

Мы находим момент времени t3, когда проекции скоростей точек становятся одинаковыми, путем нахождения пересечения двух графиков. Этот момент времени показывает, когда точки встретятся.

После нахождения момента времени t3, мы можем использовать формулу для расстояния, чтобы найти расстояние от места начала движения до места встречи. Для этого нам нужно знать скорость и время движения до момента встречи.

Однако, в данном случае у нас нет значений для скоростей точек и времени на графике. Поэтому нельзя дать точный численный ответ на этот вопрос. Но, имея графики и описание движения точек, мы можем утверждать, что расстояние между точками увеличивается с течением времени до момента t3, и будет уменьшаться после этого момента, когда точки встретятся или столкнутся.