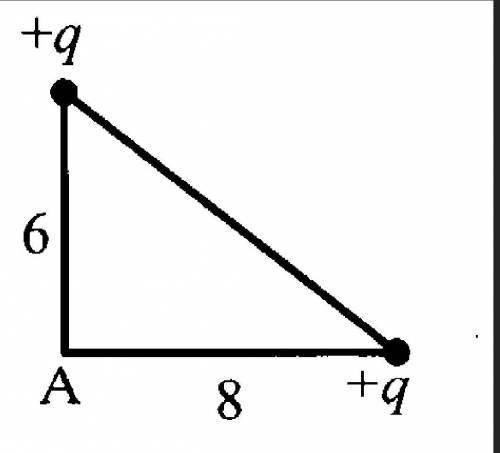
Два одинаковых положительных заряда +q и +q находятся в вершинах прямоугольного треугольника. Определите результирующую напряженность в точке А, если катеты треугольника равны 6 и 8 м. (см.рис.)
Другие вопросы по теме Физика
Популярные вопросы
- Какая сила тока в спирали электролампочки, включенной в сеть...
1 - Антон забыл кодовый номер своей банковской магнитной карты, но...
3 - 10. поезд должен пройти расстояние в 120 км между двумя с некоторой...
3 - Продолжи рассказ так,чтобы было понятно,что настя-воспитанная...
3 - Самолет вылетел из берлина на запад в 7: 00, 20 сентября. через...
3 - Тело брошено вертикально вверх со скоростью 12 м/c. на какой...
3 - Когда наступил и закончился палеолит,мезолит,неолит и т.д.?...
3 - Устовная грамота российской империи .укажите прогрессивные и...
3 - Работая один насос может откачать 1512л.воды за12ч.а вместе с...
2 - Написать структурную формулу 1,1,1- трифтор-2 -бромэтан...
2
В данной задаче у нас имеется два одинаковых положительных заряда +q и +q, расположенных на вершинах прямоугольного треугольника. Поскольку заряды положительные, напряженность идет от каждого заряда в направлении от него самого.
Шаг 1: Определим напряженность от зарядов до точки А
Пусть точка B - вершина треугольника, где находится заряд +q1, а точка C - вершина треугольника, где находится заряд +q2.
Для начала рассчитаем напряженность вектора EB (напряженность от заряда +q1 до точки А):
Напряженность вектора EB равна:
E1 = k*q1/r1^2
где k - постоянная Кулона, q1 - заряд +q1, r1 - расстояние между зарядом +q1 и точкой А.
Применим теорему Пифагора для нахождения расстояния r1:
r1^2 = BC^2 + AC^2
r1^2 = 6^2 + 8^2
r1^2 = 36 + 64
r1^2 = 100
r1 = 10 м
Теперь подставим найденное значение r1 в формулу для E1:
E1 = k*q1/r1^2
E1 = (9*10^9 N*m^2/C^2) * q1 / (10 м)^2
Аналогично, напряженность вектора EC (напряженность от заряда +q2 до точки А):
Напряженность вектора EC равна:
E2 = k*q2/r2^2
где k - постоянная Кулона, q2 - заряд +q2, r2 - расстояние между зарядом +q2 и точкой А.
Применим теорему Пифагора для нахождения расстояния r2:
r2^2 = AB^2 + AC^2
r2^2 = 8^2 + 6^2
r2^2 = 64 + 36
r2^2 = 100
r2 = 10 м
Теперь подставим найденное значение r2 в формулу для E2:
E2 = k*q2/r2^2
E2 = (9*10^9 N*m^2/C^2) * q2 / (10 м)^2
Шаг 2: Вычисляем результирующую напряженность в точке А
Результирующая напряженность в точке А равна сумме напряженностей векторов EB и EC:
E = E1 + E2
Подставляем значения E1 и E2:
E = (9*10^9 N*m^2/C^2) * q1 / (10 м)^2 + (9*10^9 N*m^2/C^2) * q2 / (10 м)^2
Если векторы напряженностей EB и EC направлены вдоль осей координат, то результирующая напряженность также будет иметь направление вдоль осей координат.
Это решение позволяет определить только модуль результирующей напряженности в точке А. Чтобы определить направление, необходимо знать угол между векторами EB и EC. Если треугольник равносторонний, то угол между векторами будет 60 градусов.
Итак, модуль результирующей напряженности в точке А равен E = (9*10^9 N*m^2/C^2) * q1 / (10 м)^2 + (9*10^9 N*m^2/C^2) * q2 / (10 м)^2.