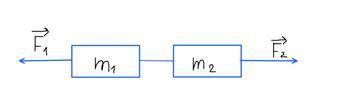
Два бруска массами m1 = 2 кг и m2 = 3 кг, связанные лёгкой нерастяжимой нитью, находятся на гладкой горизонтальной плоскости (см. рисунок). К ним приложены силы F1 = 2 Н и F2 = 10 Н. Найдите модуль ускорения системы этих тел. (В ответе напишите просто цифру. Единица измерения метр на секунду в квадрате.)

Хорошо, давайте решим эту задачу шаг за шагом.

1. Сначала найдем силу натяжения нити T. Поскольку нить нерастяжимая и связывает оба бруска, сила натяжения будет одинаковой для обоих брусков. Для этого можем воспользоваться уравнением равновесия по вертикали:
F1 + T - m1*g = 0 (1)
где F1 - сила, приложенная к первому бруску,
T - сила натяжения нити,
m1 - масса первого бруска,
g - ускорение свободного падения.

2. Теперь применим уравнение равновесия по горизонтали. Поскольку бруски находятся на гладкой поверхности, нет силы трения. Значит, сумма горизонтальных сил равна нулю:
T - F2 - µ*m2*g = 0 (2)
где F2 - сила, приложенная ко второму бруску,
µ - коэффициент трения между брусками (равен нулю в данной задаче, так как говорится, что поверхность гладкая),
m2 - масса второго бруска,
g - ускорение свободного падения.

3. Теперь нужно решить систему уравнений (1) и (2) для нахождения неизвестных T и g.

Из уравнения (1), можем выразить T:
T = m1*g - F1

Подставим это значение T в уравнение (2):
m1*g - F1 - F2 - µ*m2*g = 0

Выразим g отсюда:
m1*g - µ*m2*g = F1 + F2
g*(m1 - µ*m2) = F1 + F2
g = (F1 + F2) / (m1 - µ*m2)

4. Подставим известные значения в формулу и рассчитаем модуль ускорения системы этих тел:
m1 = 2 кг,
m2 = 3 кг,
F1 = 2 Н,
F2 = 10 Н,
µ = 0 (поверхность гладкая).

g = (2 + 10) / (2 - 0*3) = 12 / 2 = 6 м/с^2

Таким образом, модуль ускорения системы этих тел равен 6 м/с^2.