Для поражения цели с самолёта запускают ракету. самолёт летит горизонтально на высоте н = 8 км со скоростью v0 = 300 м/с. масса ракеты изменяется по закону m = m0ехр(-lambdat) и уменьшается за время полёта к цели в е раз. скорость истечения газов относительно ракеты u = 1000 м/с, корпус ракеты во время её полёта горизонтален. каково расстояние l от цели до точки, над которой находился самолёт в момент запуска ракеты? сопротивление воздуха не учитывать.
ответ l = 32 кимлометра
Другие вопросы по теме Физика
Популярные вопросы
- Расставьте знаки препинания: укажите все цифры, на месте которых в предложении должны...
3 - Параллельно соединённые с сопротивлениями r = 25 ом и 2r соединены последовательно...
2 - Вкаких известных фильмах и сценах проявляется нравственность?...
2 - Решите уравнения ! у меня времени в обрез! нужно плакат делать! у меня времени правда...
3 - Укажите число,противоположное числу -m если: а)-m=3; б)-m=-6; в)-m=+5,1; г)-m=0...
2 - Выразите в радианной мере величины углов: 46,38,179 и желательно объясните как находить...
2 - Написати твір про літні канікули на 10-15 речень...
3 - Укажите словосочетания с нарушением морфологических норм. 1.черное кофе без сахара...
1 - Один рабочий изготовляет 15 деталей в час , а другой на 3 деталей меньше .сколько...
1 - Можно ли вести хозяйственную деятельность, не изменяя природу. как на ваш взгляд...
2
32 км
Объяснение:
На движение в вертикальном направлении ничего не влияет, время падения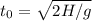 . С другой стороны, за это время масса уменьшилась в
. С другой стороны, за это время масса уменьшилась в  раз, так что
раз, так что 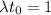 .
.
Записываем закон сохранения горизонтальной компоненты импульса (как обычно, выкидываем слагаемые второй степени малости):
Делим обе части на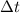 , переходим к пределу при
, переходим к пределу при  и получаем
и получаем
Йеху, да это же движение с постоянным ускорением! Начальная скорость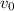 , время известно, остаётся только подставить в школьную формулу
, время известно, остаётся только подставить в школьную формулу