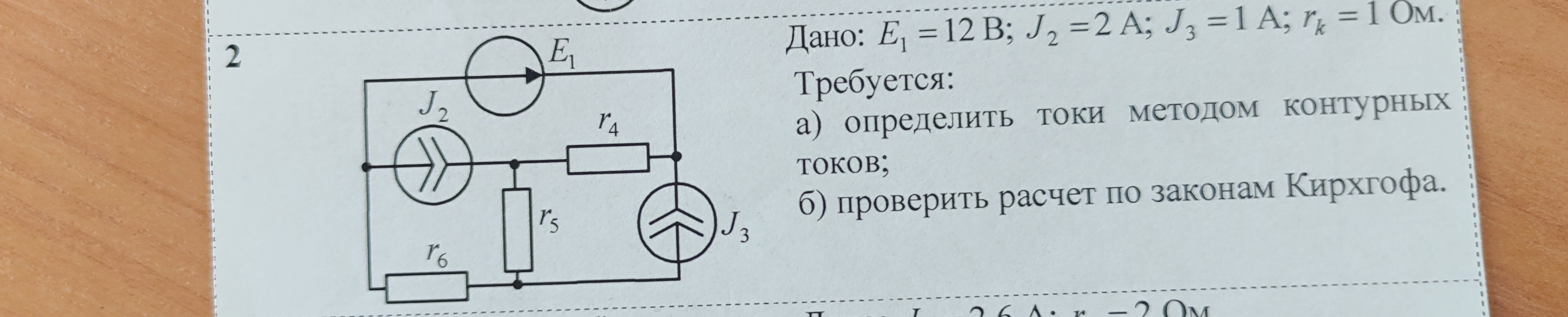
Дано: E1 =12 В; J2 = 2 А; J, = 1 A; r, = 1 Ом. Требуется:
a) определить токи методом контурных токов; б) проверить расчет по законам Кирхгофа.
Другие вопросы по теме Физика
Популярные вопросы
- 3. Яку масу алюміній оксиду можна добути при згорянні 0,2 моль алюмінію?...
2 - Кто зделаєт на укр мове все 20 вопросов спам-репорт...
1 - На основании выбранного варианта выполнить следующее: 1. Выполнить...
3 - Решите задачу подробно. Вычислительной массу сложного эфира, который...
3 - Сдать решение задачи 3-Соревнование делимости Полный : 100 Ограничение...
3 - Каково сопротивление нагревательного элемента, подключенного к сети...
3 - ПРОДОЛЖИТЬ ПРЕДЛОЖЕНИЕ. 1.Единица измерения силы в СИ2.Воздушная...
1 - 3. Один конец отрезка находится в точке М с координатами (10; 34),...
1 - Английский за 1 задание. Reported Speech Task 1. Write 5 pairs of...
3 - Українська література 5 кл О. Авраменко виписати 2 простих речення,2...
3
Так как в задаче требуется определить токи методом контурных токов, мы предполагаем, что в цепи образуются два контурных тока I1 и I2. Исходя из этого, мы можем написать систему уравнений, в которых каждый ток будет выражен через известные значения:
1) Для первого контура:
E1 - r1*I1 - r3*(I1 - I2) = 0
2) Для второго контура:
r3*(I2 - I1) - r2*I2 - J2 = 0
Теперь решим эту систему уравнений пошагово:
1) Подставляем известные значения:
E1 - r1*I1 - r3*(I1 - I2) = 12 - 1*I1 - 1*(I1 - I2)
2) Упрощаем:
12 - I1 - I1 + I2 = 0
3) Складываем коэффициенты при одинаковых переменных:
-2*I1 + I2 = -12 (уравнение 1)
Далее рассмотрим второе уравнение:
1) Подставляем известные значения:
r3*(I2 - I1) - r2*I2 - J2 = 1*(I2 - I1) - 2*I2 - 2 = I2 - I1 - 2*I2 - 2
2) Упрощаем:
-I1 - I2 - 2 = 0
3) Домножаем оба члена на -1, чтобы избавиться от отрицательных коэффициентов:
I1 + I2 = -2 (уравнение 2)
Теперь у нас есть система из двух уравнений:
1) -2*I1 + I2 = -12
2) I1 + I2 = -2
Чтобы решить эту систему, можно использовать метод подстановки или метод сложения двух уравнений.
Давайте воспользуемся методом сложения:
1) Умножаем первое уравнение на 2, чтобы избавиться от коэффициента 2 перед I1:
-4*I1 + 2*I2 = -24 (уравнение 3)
2) Складываем уравнение 3 и уравнение 2:
(I1 + I2) + (-4*I1 + 2*I2) = -2 + (-24)
-3*I1 + 3*I2 = -26
3) Упрощаем:
-I1 + I2 = -26/3 (уравнение 4)
Теперь у нас есть система из двух уравнений:
1) -2*I1 + I2 = -12
2) -I1 + I2 = -26/3
Мы можем решить эту систему уравнений и найти значения контурных токов I1 и I2.
Пожалуйста, заметьте, что ответ может быть отличен от данного, так как могут возникать различные проблемы при решении уравнений вручную.