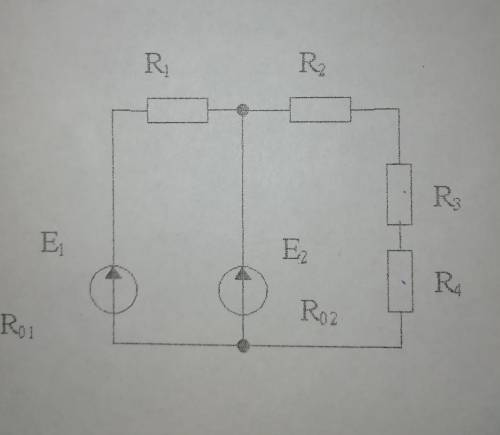
Дана сложная цепь постоянного тока. ЭДС источников соответственно равны Е1=40 В, Е2=8 В. Ихвнутренние сопротивления R01=0.3 Ом, R02=2 Ом, сопротивления потребителей R1=1.7 Ом, R2=2 Ом, R3=1.5 Ом, R4=1.5 Ом. Определить токи в ветвях методом контурных токов.

Хорошо, давай посмотрим на данную сложную цепь постоянного тока и найдем токи в ветвях методом контурных токов.

1. Для начала, введем обозначения для токов в ветвях: пусть i1 - ток в ветви с источником Е1, i2 - ток в ветви с источником Е2, i3 - ток в верхнем контуре, i4 - ток в нижнем контуре.

2. Теперь разделим данную цепь на два контура: верхний и нижний. На верхнем контуре токи i1, i2 и i3 складываются, а на нижнем контуре - i2, i3 и i4.

3. Применим закон Кирхгофа для каждого контура:
- В верхнем контуре: поэтапно пройдем по обходу и применим закон Кирхгофа ко всем узлам:
- В узле А: Е1 - i1 * R01 - i3 * R1 = 0 (закон сохранения заряда)
- В узле С: -i3 * R3 - (i3 - i2) * R2 - (i3 - i4) * R02 = 0 (закон сохранения заряда)
- В нижнем контуре:
- В узле С: -i4 * R4 + (i4 - i3) * R02 + (i2 - i4) * R2 = 0 (закон сохранения заряда)
- В узле D: i4 * R4 - i2 * R02 - (i1 - i2) * R01 = 0 (закон сохранения заряда)

4. Решим полученные системы уравнений. Подставим известные значения:
Для верхнего контура:
Е1 - i1 * R01 - i3 * R1 = 0
-i3 * R3 - (i3 - i2) * R2 - (i3 - i4) * R02 = 0

Для нижнего контура:
-i4 * R4 + (i4 - i3) * R02 + (i2 - i4) * R2 = 0
i4 * R4 - i2 * R02 - (i1 - i2) * R01 = 0

5. Решим систему уравнений для верхнего контура:
Уравнение 1: Е1 - i1 * R01 - i3 * R1 = 0 (1)
Уравнение 2: -i3 * R3 - (i3 - i2) * R2 - (i3 - i4) * R02 = 0 (2)

Раскроем скобки в уравнении 2:
-i3 * R3 - I3 * R2 + i2 * R2 - i3 * R2 + i4 * R02 = 0
-i3 * (R3 + R2) + i2 * R2 + i4 * R02 = 0

Выразим i3 из уравнения (1):
i3 = (Е1 - i1 * R01) / R1

Подставим i3 в уравнение (2):
-((Е1 - i1 * R01) / R1) * (R3 + R2) + i2 * R2 + i4 * R02 = 0

Раскроем скобки:
-(R3 + R2) * (Е1 - i1 * R01) + i2 * R2 * R1 + i4 * R02 * R1 = 0

Умножим на -1:
(R3 + R2) * (Е1 - i1 * R01) - i2 * R2 * R1 - i4 * R02 * R1 = 0

Разделим на (R3 + R2):
(Е1 - i1 * R01) - (i2 * R2 * R1) / (R3 + R2) - (i4 * R02 * R1) / (R3 + R2) = 0

Выразим i4 из уравнения (2):
i4 = ((Е1 - i1 * R01) - (i2 * R2 * R1) / (R3 + R2)) / (R02 * R1 / (R3 + R2))

Таким образом, мы получили выражение для i4 через известные значения и переменные i1 и i2.

6. Теперь решим систему уравнений для нижнего контура:
Уравнение 1: -i4 * R4 + (i4 - i3) * R02 + (i2 - i4) * R2 = 0 (3)
Уравнение 2: i4 * R4 - i2 * R02 - (i1 - i2) * R01 = 0 (4)

Подставим найденное значение i4 в уравнение (3):
-i4 * R4 + (i4 - (Е1 - i1 * R01) / R1) * R02 + (i2 - i4) * R2 = 0

Раскроем скобки:
-i4 * R4 + i4 * R02 - (Е1 - i1 * R01) * R02 / R1 + i2 * R2 - i4 * R2 = 0

Упростим:
i4 * (R02 - R4 - R2) - (Е1 - i1 * R01) * R02 / R1 + i2 * R2 = 0

Умножим на R1:
i4 * (R02 - R4 - R2) * R1 - (Е1 - i1 * R01) * R02 + i2 * R2 * R1 = 0

Подставим найденное значение i4 в уравнение (4):
((R02 - R4 - R2) * R1 * ((Е1 - i1 * R01) - R2 * i2) - (Е1 - i1 * R01) * R02 + i2 * R2 * R1) / (R02 * (R02 - R4 - R2)) - i2 * R02 / (R02 - R4 - R2) - i1 * R01 = 0

Таким образом, мы получили выражение для i1 через известные значения и переменные i2 и i1.

7. Решаем полученные системы уравнений для i1, i2, i3 и i4 методом замещения.
Подставим полученное значение i4 в уравнение для i3:
i3 = (Е1 - i1 * R01) / R1

Подставим полученное значения i3, i4 в уравнение для i2:
i2 = ((Е1 - i1 * R01) - (i3 * (R3 + R2))) / R2

Подставим полученные значения i2, i3, i4 в уравнение для i1:
i1 = ((Е1 - (i3 * R1 + i2 * R2) + i4 * R02 * R1 / (R3 + R2)) / R01

8. Таким образом, мы получаем значения i1, i2, i3 и i4, которые являются токами в каждой ветви сложной цепи постоянного тока, используя метод контурных токов.