Частота колебаний пружинного маятника равна 12 гц. если массу груза при неизменной жесткости пружины увлечить в 4раза, то частота колебаний станет равной
Ответы
Период колебаний пружинного маятника рассчитывается по формуле 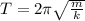 . Узнаем, во сколько раз увеличился период колебаний при увеличении массы груза.
. Узнаем, во сколько раз увеличился период колебаний при увеличении массы груза. 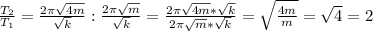 . Период увеличился в два раза. Это значит, что частота колебаний уменьшится в два раза (так как период и частота колебаний находятся в обратной зависимости). То есть, частота колебаний станет равна 12:2=6 герц. ответ: 6 герц.
. Период увеличился в два раза. Это значит, что частота колебаний уменьшится в два раза (так как период и частота колебаний находятся в обратной зависимости). То есть, частота колебаний станет равна 12:2=6 герц. ответ: 6 герц.
ПОКАЗАТЬ ОТВЕТЫ
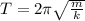 . Узнаем, во сколько раз увеличился период колебаний при увеличении массы груза.
. Узнаем, во сколько раз увеличился период колебаний при увеличении массы груза. 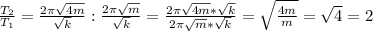 . Период увеличился в два раза. Это значит, что частота колебаний уменьшится в два раза (так как период и частота колебаний находятся в обратной зависимости). То есть, частота колебаний станет равна 12:2=6 герц. ответ: 6 герц.
. Период увеличился в два раза. Это значит, что частота колебаний уменьшится в два раза (так как период и частота колебаний находятся в обратной зависимости). То есть, частота колебаний станет равна 12:2=6 герц. ответ: 6 герц.
Другие вопросы по теме Физика
Популярные вопросы
- Запишіть Анкету трагедії Шекспіра ,,Ромео і Джульєтта ів...
3 - ПИТОН ! Можно в 1, можно в нескольких программах...
3 - 10. Які плоди характерні для родини Лілійні?...
3 - 4a-3b+20 если 2a-9b+3/2a-4b+6=3...
1 - При полной дегидратации некоторой части спирта неизвестного состава...
2 - Расскажите о имени числительном как части речи...
1 - 4. У Кирилла 2 пружины. Ваня принес грузик в 1 кг и они вместе подвесили...
3 - 0,5(l,6x - 6,4y) - 2,4(1,5x + y), якщо х = 3, у = -4,5 можно с пошаговым...
2 - Нұр-Сұлтан қаласындағы «Бәйтерек» монументінің символяли, мәні туралы...
1 - 8*21=85 3*6=15 5*7 =? 4*12=28 Это логика аа...
3