1. Физика
  2. Брусок массой 1кг лежит на наклонной

Брусок массой 1кг лежит на наклонной плоскости с углом наклона 30° к горизонту. определите силу трения, действующую на брусок, если коэффициент трения равен 0,4.

banilchik26 banilchik26    1   27.09.2019 04:30    7

Ответы
ГрознаяВафля ГрознаяВафля  08.10.2020 21:55

Дано:

m = 1 кг

\alpha = 30^{\circ}

g = 10 м/с²

v = 0 м/с ⇒ a = 0 м/с²

\mu = 0,4

====================

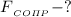
Найти: F{_{_{CO\varPi P}}} - ?

====================

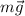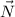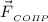Решение. На брусок действуют три силы: сила тяжести m\vec{g}, сила \vec{N} нормальной реакции опоры и сила сопротивления \vec{F}{_{_{CO\varPi P}}}.

Брусок не двигается, значит, ускорение равно нулю.

Выполним пояснительный рисунок, указав на нём силы, действующие на брусок.

Свяжем систему координат с бруском на поверхности Земли, ось OY направим перпендикулярно поверхности дороги, ось ОХ - вдоль дороги (при таком выборе осей только одна сила (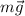m\vec{g}) не лежит на осях координат).

Запишем второй закон Ньютона в векторном виде:

\vec{F}{_{_{CO\varPi P}}} + \vec{N} + m\vec{g} = m\vec{a}

Спроецируем уравнение на оси координат (сила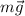 m\vec{g} не лежит на оси координат, поэтому для нахождения её проекций опустим из конца вектора 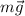m\vec{g} перпендикуляры на оси OX и OY: 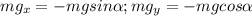mg_{x} = -mgsin\alpha; mg_{y} = -mgcos\alpha) и запишем выражение для силы сопротивления:

\left \{ {{OX:-F{_{_{CO\varPi P}}} - mgsin\alpha=0} \atop {OY: N - mgcos\alpha = 0}} \right.

F{_{_{CO\varPi P}}} = \mu N

Решив полученную систему уравнений, найдём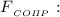 F{_{_{CO\varPi P}}}:

N = mgcos\alpha \Rightarrow \boxed {F{_{_{CO\varPi P}}} = \mu mgcos\alpha}

Определим значение искомой величины:

F{_{_{CO\varPi P}}} = 0,4 \cdotp 1 \cdotp 10 \cdotp \frac{\sqrt{3}}{2} = 2\sqrt{3} \thickapprox 3,46 H.

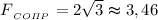ответ: F{_{_{CO\varPi P}}} = 2\sqrt{3} \thickapprox 3,46 H.


Брусок массой 1кг лежит на наклонной плоскости с углом наклона 30° к горизонту. определите силу трен
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
звезда0ютуба звезда0ютуба  16.09.2021 18:02
решить и построить график и изобразить на нем траекторию движения тела... и к графику построить табличку x,y координат...
aruzhanormanova aruzhanormanova  16.09.2021 18:02
1. Из города со скоростью 18 м/с выезжает автомобиль. Спустя 20 мин вслед за ним выезжает второй автомобиль. С какой скоростью двигался второй автомобиль, если он догнал первый спустя...
gkulgkuy gkulgkuy  16.09.2021 18:01
у вагоні потяга що рухається зі швидкістю 72 км/год у напрямку його руху йде пасажир зі швидкістю 2м/с з якою швидкістю рухається пасажир відносно залізничного полотна...
ПомощникКоторыйЛюбит ПомощникКоторыйЛюбит  16.09.2021 18:00
ціна поділки шкал яких вимірювальних приладів визначала Яринка?...
cnastya970 cnastya970  16.09.2021 17:58
ДО ІТЬ!! назвіть кілька фізичних тіл які складаються з двох або трьох фізичних речовин назвіть ці речовини ІВ БУДЬ ЛАСКА!...
Abdulmansur Abdulmansur  08.08.2019 16:50
Найти плотность тела массой 5,4 кг и обьемом 0,002 м в куберешить...
Ясмина1604 Ясмина1604  08.08.2019 16:50
Автомобиль проехал первую половину пути со скоростью 60 км/ч, а другую половину пути со скоростью 80 км/ч. найти vср...
Бубух Бубух  08.08.2019 16:50
Два тела, связанные невесомой нерастяжимой нитью тянут с силой 15 н вправо по столу. массы брусков m1= 1 кг и m2 = 4 кг, μ = 0,1. с каким ускорением движутся бруски? чему равна сила...
девчонка1999 девчонка1999  15.03.2021 14:52
Відомо що опір R¹становить 100 Ом, опір R²—150 Ом, показ амперметра2,4 АВизначте напругу на ділянці​...
vlad31106 vlad31106  15.03.2021 14:52
1 За единицу давления принимают давление, которое производит: А) масса 1 кг на 1 см²В)сила , равная 10 Н, на 1 см²С)масса 1 кг на 1 м²D)сила, равная 1 Н, на 1 м²2. Какой ученый выдвинул...

Популярные вопросы