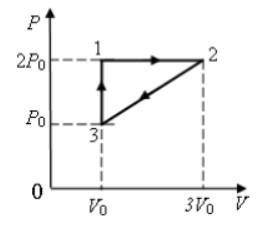
Азот совершает круговой процесс, состоящий из двух изохор и двух изобар (см. рисунок). Количество
теплоты, полученное газом Qн
в этом круговом
процессе
1) 4 P0 V0 2) 6,5 P0V0 3) 9,5 P0 V0
4) 12P0 V0

Для решения данной задачи, нам необходимо воспользоваться первым законом термодинамики. Первый закон термодинамики утверждает, что изменение внутренней энергии газа равно сумме работы, совершенной над газом и переданной ему теплоты. Рассмотрим каждый из процессов в отдельности и найдем работу и теплоту для каждого: 1. Изохорный процесс (сжатие газа при постоянном объеме): В данном процессе газ не совершает работы, так как объем остается постоянным. Следовательно, работа равна нулю (A = 0). Теплоту, полученную газом при изохорном процессе, обозначим как Q1. 2. Изобарный процесс (нагрев газа при постоянном давлении): В данном процессе газ расширяется и совершает работу против постоянного давления. Рабочим выражением для работы в изобарном процессе является формула работы: A = P * ΔV, где P - давление газа, ΔV - изменение объема газа. Так как в нашем случае газ расширяется, то он совершает положительную работу. Теплоту, полученную газом при изобарном процессе, обозначим как Q2. 3. Изохорный процесс (охлаждение газа при постоянном объеме): Как и в первом изохорном процессе, газ не совершает работы, так как объем остается постоянным. Здесь также работа равна нулю (A = 0). Теплоту, полученную газом при изохорном процессе, обозначим как Q3. 4. Изобарный процесс (сжатие газа при постоянном давлении): В данном процессе газ сжимается и совершает отрицательную работу. Так как в данном случае газ сжимается, то работа будет отрицательной. Теплоту, полученную газом при изобарном процессе, обозначим как Q4. Теперь мы можем записать уравнение первого закона термодинамики для всего кругового процесса: ΔU = Q1 + Q2 + Q3 + Q4 + A Учитывая, что изменение внутренней энергии ΔU равно нулю (так как процесс является круговым), и с учетом того, что работа в изобарном процессе равна P * ΔV, где ΔV2 = -ΔV1, получим: 0 = Q1 + Q2 + Q3 + Q4 + P * (ΔV2 - ΔV1) Так как в изохорных процессах объем остается постоянным (ΔV = 0), получим: 0 = Q2 + Q4 Теперь осталось только определить значения Q2 и Q4, и мы сможем найти общую полученную теплоту Qн в круговом процессе. Q2 - количество теплоты, полученная газом при изобарном процессе, которое можно определить, используя следующую формулу: Q2 = n * C * ΔT, где n - количество вещества (в данном случае азота), C - молярная теплоемкость газа, ΔT - изменение температуры газа. Q4 - количество теплоты, полученная газом при изобарном процессе: Q4 = -Q2 Теперь давайте рассмотрим возможные варианты ответов: 1) 4 P0 V0 2) 6,5 P0V0 3) 9,5 P0 V0 4) 12 P0 V0 Сравним каждый из вариантов ответов с нашим решением: 1) Если выбрать Q2 = 4 P0 V0, то Q4 = -4 P0 V0, и мы получим, что общая полученная теплота Qн будет равна нулю (Qн = Q2 + Q4 = 4 P0 V0 - 4 P0 V0 = 0). Этот вариант ответа неверный. 2) Если выбрать Q2 = 6,5 P0 V0, то Q4 = -6,5 P0 V0, и мы получим, что общая полученная теплота Qн будет равна нулю (Qн = Q2 + Q4 = 6,5 P0 V0 - 6,5 P0 V0 = 0). Этот вариант ответа неверный. 3) Если выбрать Q2 = 9,5 P0 V0, то Q4 = -9,5 P0 V0, и мы получим, что общая полученная теплота Qн будет равна нулю (Qн = Q2 + Q4 = 9,5 P0 V0 - 9,5 P0 V0 = 0). Этот вариант ответа неверный. 4) Если выбрать Q2 = 12 P0 V0, то Q4 = -12 P0 V0, и мы получим, что общая полученная теплота Qн будет равна нулю (Qн = Q2 + Q4 = 12 P0 V0 - 12 P0 V0 = 0). Этот вариант ответа неверный. Таким образом, ни один из предложенных вариантов ответов не является правильным. Верный ответ в данном случае неизвестен или не представлен.