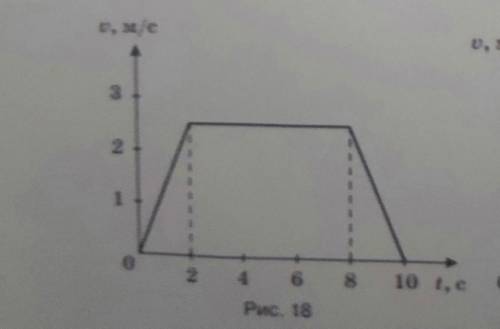
A13. На рис.18 представлен график скорости материальной точки. Путь, пройденный точкой в интервале времени от 4 до 8 с, равен​

Для решения данной задачи, нам необходимо проанализировать график скорости материальной точки и найти путь, пройденный точкой в интервале времени от 4 до 8 с.

1. Посмотрим на оси графика. На оси X отложено время (временной интервал), а на оси Y отложена скорость материальной точки.

2. Изучим график в интервале времени от 4 до 8 с. Учитывая, что на графике представлена скорость, основной момент, который нам нужно сделать - это найти площадь под кривой в заданном интервале. Площадь под графиком скорости в заданном интервале равна пути, пройденному материальной точкой.

3. Подсчитаем площадь под графиком в заданном интервале. Для этого разобьем этот интервал на две части (4-6 с и 6-8 с), так как скорость меняется в рамках каждого из этих интервалов.

- Найдем площадь под графиком в интервале времени от 4 до 6 с. Для этого нужно найти площадь прямоугольника, ограниченного графиком скорости, осью времени и двумя прямыми, перпендикулярными оси времени и проходящими через начальную и конечную точки отрезка времени. В данном случае, площадь этого прямоугольника равна 2 м/с * 2 с = 4 м.

- Найдем площадь под графиком в интервале времени от 6 до 8 с. Площадь этого прямоугольника равна 3 м/с * 2 с = 6 м.

4. Теперь, чтобы найти путь, пройденный точкой в интервале времени от 4 до 8 с, нужно сложить площади прямоугольников, которые мы посчитали на предыдущем шаге. В данном случае, получаем 4 м + 6 м = 10 м.

Ответ: Путь, пройденный точкой в интервале времени от 4 до 8 с, равен 10 м.