А) Тело бросили с земли вертикально вверх со скоростью 5 м/c.
Какой максимальной высоты оно достигло? Сопротивление
воздуха не учитывать.
б) Тело свободно падает с высоты 20 м. На какой высоте его
потенциальная энергия в 2 раза меньше кинетической?
Другие вопросы по теме Физика
Популярные вопросы
- Самая большая планета солнечной системы?...
2 - 40 . жду уже 3 дня. сравните карское и чёрное море по плану: 1.к бассейну...
3 - Из двух городов, расстояние между которыми 300 км, одновременно навстречу...
3 - Сформулируйте определение прямой пропорциональной...
3 - a представьте себя через 15 лет. 1.five things that you may do. 5 вещей,...
2 - Два куска металла имеют одинаковый объём но разную массу. что можно сказать...
1 - При сортировке помидоров незрелые составили одну десятую часть от собранных...
3 - Внекотором царстве для написания слов используют только 18 букв. найти...
1 - Как правильно пишется примёрзший или премёрзший?...
2 - Укажи породы собак? лабрадор? такса? перс? овчарка?...
3
а) 1,25 м
б) 6,67 м
Объяснение:
а) По сути, движение брошенного вверх тела — это равноускоренное движение с отрицательным ускорением g (ускорением свободного падения), поэтому перемещение тела (равное максимальной высоте подъёма) можно выразить формулой
В данном случае v = 0, так как на максимальной высоте тело останавливается (и потом начинает падать вниз), v0 = 5 м/с, ускорение а — ускорение свободного падения g. Но так как тело движется вверх, а g направлено вниз, то есть ускорение направлено противоположно движению, g приобретает знак «минус». Тогда формулу перемещения можно переписать как
Подставим значения величин из условия:
ответ: 1,25 м.
б) Потенциальная энергия тела вычисляется по формуле Еп = m*g*h (m — масса тела, h — высота, на которой оно находится), а кинетическая энергия — по формуле Ек =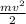
На искомой высоте h выполняется равенство
Ек = 2Еп, то есть
Разделив обе части равенства на m, получим
Назовём путь, который тело, чтобы набрать скорость v, буквой L. Так как свободное падение — это равноускоренное движение с ускорением g,
(v0 = 0; g положительно, так как оно направлено вниз, и тело тоже движется вниз).
Пусть h — искомая высота, на которой Ек = 2Еп, Н — максимальная высота (та, с которой падает тело; по условию, Н=20 м). Так как для соблюдения условия Ек = 2Еп нужно, чтобы тело набрало скорость v, а эту скорость оно набирает, пройдя путь L,
h = H - L =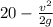
Итак,
Подставим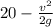 вместо h в уравнение скорости:
вместо h в уравнение скорости:
Возведём обе части в квадрат:
Подставим это значение в формулу для h:
Проверим, выполняется ли условие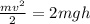 :
:
133,3m ≈ 133,4m
[расхождение появляется из-за того, что g взято равным 10 м/с2, а не 9,8 м/с2, и прочих округлений; расхождение не сильно влияет на результат]
ответ: 6,67 м.