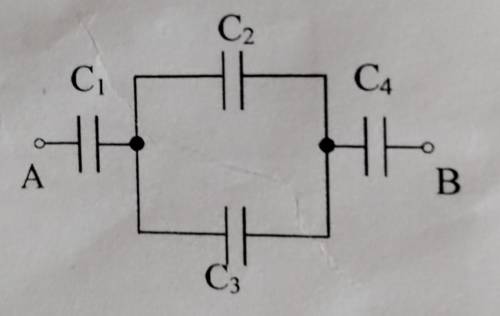
3. Четыре конденсатора емкостями С1 = С2 = 1 мкФ, С3 = 3 мкФ, С4 = 2 соединены как показано на рисунке. К точкам А и В подводится напряжение 140 В. Определите заряд q и напряжение U, на каждом из конденсаторов

Для решения данной задачи, мы можем использовать закон сохранения заряда и закон сохранения энергии.

Шаг 1: Определение зарядов на каждом конденсаторе
Поскольку все конденсаторы соединены параллельно, заряд на каждом конденсаторе будет одинаковым. Обозначим этот заряд как q.

Шаг 2: Определение напряжения на каждом конденсаторе
Напряжение на конденсаторе можно определить с использованием формулы для энергии на конденсаторе (E = 1/2 * C * V^2), где C - емкость конденсатора, V - напряжение на конденсаторе.

Для конденсатора C1 (емкость 1 мкФ):
E1 = 1/2 * 1 * V1^2 = 1/2 * 1 * (140 - U)^2, где U - напряжение на конденсаторе C1.

Для конденсатора C2 (емкость 1 мкФ):
E2 = 1/2 * 1 * V2^2 = 1/2 * 1 * (140 - U)^2, где U - напряжение на конденсаторе C2.

Для конденсатора C3 (емкость 3 мкФ):
E3 = 1/2 * 3 * V3^2 = 1/2 * 3 * (140 - U)^2, где U - напряжение на конденсаторе C3.

Для конденсатора C3 (емкость 2 мкФ):
E4 = 1/2 * 2 * V4^2 = 1/2 * 2 * U^2, где U - напряжение на конденсаторе C4.

Шаг 3: Закон сохранения заряда
Заряд на каждом конденсаторе равен суммарному заряду, т.е. q = q1 + q2 + q3 + q4, где q1-q4 - заряды на соответствующих конденсаторах.

Шаг 4: Запись уравнений
Теперь мы можем записать систему уравнений, используя закон сохранения энергии и закон сохранения заряда:

1. q1 = q2 + q3
2. q3 = q4 + q

3. E1 = E2 + E3
4. E3 = E4 + U

где E1-E4 - энергии на соответствующих конденсаторах.

Шаг 5: Решение системы уравнений
Подставим выражения для энергий из шага 2 в уравнения 3 и 4:

1/2 * 1 * (140 - U)^2 = 1/2 * 1 * (140 - U)^2 + 1/2 * 3 * (140 - U)^2
1/2 * 3 * (140 - U)^2 = 1/2 * 2 * U^2 + U

Приведем уравнения к более простому виду:

(140 - U)^2 = (140 - U)^2 + 3 * (140 - U)^2
3 * (140 - U)^2 = 2 * U^2 + 2 * U

Произведем раскрытие скобок и сокращение:

4200 - 420U + U^2 = 140U^2 + 2U^2 + 2U
150U^2 - 420U - 4200 = 0

Шаг 6: Решение квадратного уравнения
Данное уравнение является квадратным, поэтому мы можем использовать квадратное уравнение для его решения. Решив уравнение, мы найдем значения напряжения U на конденсаторе C4.

U = (-b ± √(b^2 - 4ac)) / 2a

где a = 150, b = -420, c = -4200.

Подставим значения и решим квадратное уравнение.

U = (-(-420) ± √((-420)^2 - 4 * 150 * -4200)) / (2 * 150)

U = (420 ± √(176400 + 2520000)) / 300

U = (420 ± √(2696400)) / 300

U = (420 ± 1640) / 300

Итак, мы получаем два решения:

U1 = (420 + 1640) / 300 = 2060 / 300 ≈ 6.87 В

U2 = (420 - 1640) / 300 = -1220 / 300 ≈ -4.07 В

Так как напряжение не может быть отрицательным, мы отбрасываем U2.

Шаг 7: Определение зарядов на конденсаторах
Теперь, когда мы знаем напряжение на конденсаторе C4, мы можем рассчитать заряды на каждом конденсаторе, используя уравнения закона сохранения заряда.

Для этого, зная напряжение U и емкость каждого конденсатора, мы можем использовать формулу Q = C * U, где Q - заряд, C - емкость, U - напряжение.

q1 = C1 * U1 = 1 * 6.87 ≈ 6.87 мкКл
q2 = C2 * U1 = 1 * 6.87 ≈ 6.87 мкКл
q3 = C3 * U1 = 3 * 6.87 ≈ 20.61 мкКл
q4 = C4 * U1 = 2 * 6.87 ≈ 13.74 мкКл

Ответ: Заряд на каждом конденсаторе составляет примерно 6.87 мкКл для C1 и C2, 20.61 мкКл для C3 и 13.74 мкКл для C4. Напряжение на каждом конденсаторе составляет примерно 6.87 В.