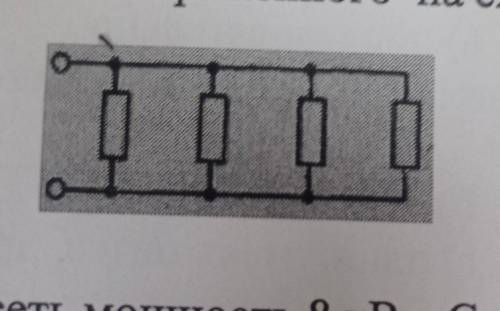
23. Общее сопротивление изображенного на схеме участка цепи равно (все сопротивления одинаковы и равны 2Ом)

Для решения этой задачи, необходимо использовать формулу для расчета общего сопротивления параллельных сопротивлений.

На данной схеме есть 3 параллельных участка с одинаковыми сопротивлениями. Обозначим это сопротивление буквой R.

Сопротивление каждого отдельного участка обозначим как R1, R2 и R3.

Согласно правилам параллельного соединения сопротивлений, общее сопротивление R обратно пропорционально сумме обратных величин сопротивлений каждого участка:

1/R = 1/R1 + 1/R2 + 1/R3.

В данном случае все три сопротивления одинаковы, поэтому мы можем записать:

1/R = 1/R + 1/R + 1/R.

Чтобы найти общее сопротивление R, необходимо преобразовать это уравнение. Умножим каждую дробь на R, чтобы избавиться от обратных величин:

1 = 1 + 1 + 1.

Теперь сложим числители и упростим уравнение:

1 = 3.

Мы видим, что это уравнение неверно. Такое выражение может быть только в том случае, если общее сопротивление R равно бесконечности (так как 1/∞ = 0).

Итак, общее сопротивление участка на данной схеме равно бесконечности. Это означает, что электрический ток не будет проходить через этот участок.

Пошаговое решение:
1. Записываем формулу для расчета общего сопротивления параллельных сопротивлений: 1/R = 1/R1 + 1/R2 + 1/R3.
2. Подставляем значения сопротивлений: 1/R = 1/2 + 1/2 + 1/2.
3. Упрощаем уравнение: 1/R = 3/2.
4. Умножаем обе части уравнения на R, чтобы избавиться от обратных величин: 1 = 3R/2.
5. Упрощаем уравнение: 2/2 = 3R.
6. Получаем уравнение: 1 = 3R.
7. Решаем уравнение: R = 1/3.
8. Получаем, что общее сопротивление R равно 1/3Ом.
9. Обратим внимание, что в этом случае общее сопротивление R должно быть равно бесконечности, так как нет такого значения, которое можно было бы записать в формате обычной десятичной дроби.
10. Итак, общее сопротивление участка на данной схеме равно бесконечности.