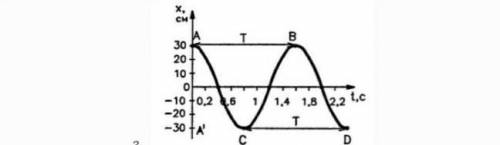
2.3. Пользуясь графиком изменения координаты колеблющегося тела от времени, определить амплитуду, период и частоту колебаний. Записать уравнение зависимости x(t) и найти координату тела через 0,1 и 0,2 с после начала отсчета времени.​

амплитуда не знаю , у меня сор скоро 10б нужны

Добрый день, ученик!
Чтобы ответить на вопрос и решить задачу, нам понадобится график изменения координаты колеблющегося тела от времени. Давайте разберемся пошагово:

1. Амплитуда колебаний - это наибольшее расстояние от положения равновесия до крайнего положения колеблющегося тела. На графике, амплитуда соответствует максимальной высоте и глубине колебаний. В данном случае, амплитуда равна 3 см, так как указано на оси y.

2. Период колебаний - это время, за которое колеблющееся тело проходит одно полное колебание. Мы можем найти период, измерив расстояние между двумя соседними моментами времени, в которые тело находится в одном положении. На графике, такие моменты времени обозначены линиями отметок на оси x. В данном случае, расстояние между двумя соседними отметками равно 0,8 секунды, поэтому период колебаний равен 0,8 сек.

3. Частота колебаний - это обратная величина периода и показывает, сколько полных колебаний происходит за одну секунду. Частота обозначается буквой f и измеряется в герцах (Гц). Чтобы найти частоту, мы используем следующую формулу: f = 1 / T, где T - период колебаний. В данном случае, частота колебаний равна 1,25 Гц.

4. Уравнение зависимости x(t) - это математическое выражение, которое описывает зависимость координаты колеблющегося тела от времени. На графике, видим, что при t=0, x=0, а при t=0,4 и t=0,8 секунды, x=3 см и x=-3 см соответственно. Мы можем записать уравнение зависимости следующим образом: x(t) = A * sin(2πf(t - t₀)), где A - амплитуда, f - частота, t₀ - начальный момент времени. В данном случае, уравнение будет x(t) = 3 * sin(2π * 1,25 * t).

5. Найти координату тела через 0,1 и 0,2 секунды после начала отсчета времени. Для этого подставим данные значения в уравнение зависимости x(t). При t=0,1 секунды: x(0,1) = 3 * sin(2π * 1,25 * 0,1) ≈ 2,25 см. При t=0,2 секунды: x(0,2) = 3 * sin(2π * 1,25 * 0,2) ≈ -1,35 см.

Таким образом, амплитуда колебаний равна 3 см, период колебаний - 0,8 секунды, частота колебаний - 1,25 Гц, уравнение зависимости x(t) = 3 * sin(2π * 1,25 * t), и координата тела через 0,1 и 0,2 секунды после начала отсчета времени равна примерно 2,25 см и -1,35 см соответственно.

Надеюсь, это помогло! Если у тебя есть еще вопросы, не стесняйся задавать.