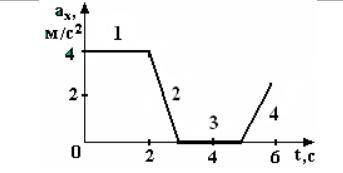
1) На рисунке 1 представлен график зависимости проекции ускорения ах от времени t для материальной точки, движущейся вдоль оси ОХ. Начальная скорость движения точки V0х = –2 м/с. Проекция скорости Vх движущейся точки в момент времени 3 с равна …м/с. 2) Движение тела вокруг неподвижной оси вращения задано уравнением φ=π(9t-3t^2),рад. Сколько оборотов N сделает тело до момента изменения направления вращения тела и чему равна средняя угловая скорость тела за этот интервал времени?

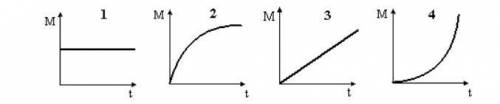
3) Момент импульса тела относительно неподвижной оси изменяется по закону L=at. Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело. (рисунок 2)

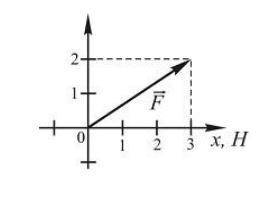
4) На рисунке показан вектор силы (в Ньютонах), действующей на частицу. Найти работу, совершенную этой силой при перемещении частицы из начала координат в точку с координатами (5; 2), м. (рисунок 3)

1) Чтобы найти проекцию скорости Vx в момент времени 3 секунды, нужно найти площадь под графиком ускорения от начального момента времени до 3 секунды и поделить на промежуток времени.

На графике ускорения ах представлено отрицательное значение ускорения от начального момента времени (t = 0) до момента времени 3 секунды. Таким образом, точка движется в отрицательном направлении по оси OX.

Итак, чтобы найти проекцию скорости Vx в момент времени 3 секунды, мы должны найти площадь треугольника, образованного графиком ускорения от начального момента времени до 3 секунды, а затем разделить эту площадь на промежуток времени.

По графику видно, что ускорение линейно увеличивается от -4 м/с² до -8 м/с² за промежуток от 0 до 3 секунд. Также известно, что начальная скорость V0x = -2 м/с.

Площадь треугольника равна половине произведения основания и высоты. Основание равно 3 секунды, а высота равна изменению ускорения за этот промежуток времени: Δах = (-8 м/с²) - (-4 м/с²) = -4 м/с².

Таким образом, площадь треугольника равна (1/2) * 3 сек * (-4 м/с²) = -6 м/с.

Теперь мы можем найти проекцию скорости Vx в момент времени 3 секунды, разделив площадь треугольника на промежуток времени: Vx = (-6 м/с) / 3 с = -2 м/с.

Ответ: Проекция скорости Vx движущейся точки в момент времени 3 секунды равна -2 м/с.

2) Дано уравнение φ=π(9t-3t^2), рад. Здесь φ обозначает угол поворота, а t - время.

Чтобы найти количество оборотов N, сделанных телом до момента изменения направления вращения, мы должны найти значения времени t, при которых угол поворота φ меняется на π, то есть φ=π.

Итак, преобразуем уравнение: φ=π(9t-3t^2) = 9πt - 3πt^2 = π.

3πt^2 - 9πt + π = 0.

Решая это квадратное уравнение, мы найдем два значения времени t, при которых угол поворота равен π.

После нахождения этих значений времени t, мы можем вычислить количество оборотов N до момента изменения направления вращения. В данном случае, количество оборотов равно количеству решений квадратного уравнения.

Чтобы найти среднюю угловую скорость тела за этот интервал времени, мы используем формулу: средняя угловая скорость = изменение угла поворота / промежуток времени.

Из уравнения φ=π(9t-3t^2), мы знаем, что τ (изменение угла поворота) = π - 0 = π (рад). А промежуток времени Δt равен разности временных точек, в которых происходит изменение угла поворота.

Ответ: Чтобы найти количество оборотов N, сделанных телом до момента изменения направления вращения, необходимо решить квадратное уравнение 3πt^2 - 9πt + π = 0. Количество решений этого уравнения будет равно количеству оборотов N.
Чтобы найти среднюю угловую скорость тела за этот интервал времени, используется формула: средняя угловая скорость = изменение угла поворота / промежуток времени.

3) Дано, что момент импульса (L) тела относительно неподвижной оси изменяется по закону L=at.

Момент силы (M) определяется как производная момента импульса по времени: M = dL/dt.

Если у нас есть график, отражающий зависимость момента импульса от времени, мы можем найти график, отражающий зависимость момента силы от времени, путем нахождения производной.

График момента силы будет представлять собой график производной графика момента импульса. Если график момента импульса представляет собой прямую линию, то график момента силы будет представлять собой горизонтальную прямую, так как производная постоянной величины равна нулю.

Ответ: График, правильно отражающий зависимость от времени величины момента сил, действующих на тело, будет горизонтальной прямой.

4) На графике показан вектор силы, действующей на частицу, и дано, что это вектор (5 Н, 2 Н).

Для нахождения работы, совершенной этой силой при перемещении частицы из начала координат в точку с координатами (5, 2), мы должны найти скалярное произведение вектора силы и вектора перемещения.

Скалярное произведение двух векторов A и B вычисляется по формуле: A · B = |A| * |B| * cos(θ), где |A| и |B| - длины векторов A и B, а θ - угол между ними.

Для нахождения скалярного произведения вектора силы (5 Н, 2 Н) и вектора перемещения из начала координат в точку (5, 2), мы должны найти длины этих векторов и угол между ними.

Длина вектора силы равна √((5 Н)^2 + (2 Н)^2) = √(25 + 4) = √29 Н.

Длина вектора перемещения равна √((5 м)^2 + (2 м)^2) = √(25 + 4) = √29 м.

Угол между двумя векторами можно найти, используя формулу cos(θ) = (A · B) / (|A| * |B|).

Таким образом, мы можем вычислить cos(θ) = ((5 Н * 5 м) + (2 Н * 2 м)) / (√29 Н * √29 м) = (25 + 4) / 29 = 29 / 29 = 1.

Так как cos(θ) = 1, угол θ равен 0 градусов.

Теперь мы можем найти работу, совершенную этой силой, умножив длину векторов силы и перемещения на cos(θ); Работа = √29 Н * √29 м * cos(0 градусов) = 29 Н * 29 м * 1 = 841 Н * м.

Ответ: Работа, совершенная этой силой при перемещении частицы из начала координат в точку с координатами (5, 2), равна 841 Н * м.