1. На концах однородного тонкого стержня длиной 1 м и массой 3m при- креплены маленькие шарики массами m и 2m. Определите момент инерции та- кой системы относительно оси, перпендикулярной стержню и проходящей через точку О, лежащую на оси, стержня. Принять m = 0,1 кг.

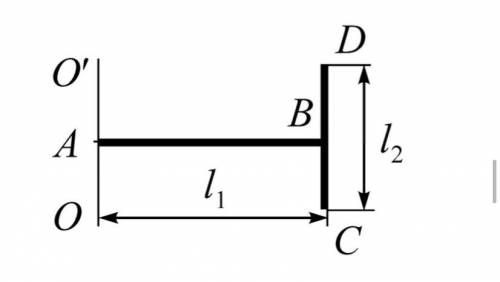
2.Два однородных тонких стержня: АВ длиной 40см и массой 900г и CD длиной 40см и массой 400г скреплены под прямым углом (рисунок). Опре-
делите момент импульса системы стержней, вращающейся с частотой ν относительно оси ОО′, прохо- дящей через конец стержня АВ параллельно стержню CD.

1. Для определения момента инерции системы относительно оси, проходящей через точку О, необходимо разделить систему на две части: стержень массой 3m и шарики массами m и 2m. Затем найдем моменты инерции каждой части и сложим их.

a) Момент инерции стержня:
Момент инерции стержня относительно оси, лежащей на конце стержня (точка О), и перпендикулярной стержню можно найти с использованием формулы момента инерции для стержня, вращающегося вокруг одного из концов:
I_стержень = (1/3) * m_стержень * L_стержень^2

где I_стержень - момент инерции стержня,
m_стержень - масса стержня,
L_стержень - длина стержня.

Подставляем известные значения:
I_стержень = (1/3) * (3m) * (1 м)^2
I_стержень = m

b) Момент инерции шариков:
Момент инерции одного шарика относительно оси, проходящей через точку О, можно найти с использованием формулы момента инерции для точечной частицы, вращающейся вокруг оси, проходящей через ее массовый центр:
I_шарик = m_шарик * r_шарика^2

где I_шарик - момент инерции шарика,
m_шарик - масса шарика,
r_шарика - расстояние от оси до шарика.

Подставляем известные значения:
I_шарик = m * r_шарика^2
I_шарик = m * (0.5 м)^2
I_шарик = 0.25 m

Так как на концах стержня прикреплены два шарика, момент инерции системы шариков будет равен сумме моментов инерции каждого шарика:
I_система_шариков = 2 * I_шарик
I_система_шариков = 2 * 0.25 m
I_система_шариков = 0.5 m

Теперь мы можем сложить моменты инерции стержня и шариков для определения момента инерции всей системы:
I_система = I_стержень + I_система_шариков
I_система = m + 0.5 m
I_система = 1.5 m

Таким образом, момент инерции системы относительно оси, перпендикулярной стержню и проходящей через точку О, равен 1.5 м.

2. Для определения момента импульса системы стержней относительно оси ОО', нужно учесть массы, длины стержней и их скорости вращения.

a) Момент импульса стержня AB:
Момент импульса стержня AB относительно оси ОО' можно найти с использованием формулы момента импульса:
L_AB = I_AB * ω_AB

где L_AB - момент импульса стержня AB,
I_AB - момент инерции стержня AB относительно оси ОО',
ω_AB - угловая скорость вращения стержня AB.

Момент инерции стержня AB относительно оси ОО' можно найти с использованием формулы момента инерции для стержня, вращающегося вокруг оси, перпендикулярной к стержню и проходящей через его конец:
I_AB = (1/3) * m_AB * L_AB^2

где m_AB - масса стержня AB,
L_AB - длина стержня AB.

Подставляем известные значения:
I_AB = (1/3) * (0.9 кг) * (0.4 м)^2
I_AB = 0.048 кг * м^2

b) Момент импульса стержня CD:
Момент импульса стержня CD относительно оси ОО' можно найти с использованием формулы момента импульса:
L_CD = I_CD * ω_CD

где L_CD - момент импульса стержня CD,
I_CD - момент инерции стержня CD относительно оси ОО',
ω_CD - угловая скорость вращения стержня CD.

Момент инерции стержня CD относительно оси ОО' можно найти с использованием формулы момента инерции для стержня, вращающегося вокруг оси, перпендикулярной к стержню и проходящей через его конец:
I_CD = (1/3) * m_CD * L_CD^2

где m_CD - масса стержня CD,
L_CD - длина стержня CD.

Подставляем известные значения:
I_CD = (1/3) * (0.4 кг) * (0.4 м)^2
I_CD = 0.021 кг * м^2

Теперь мы можем сложить моменты импульса стержней AB и CD для определения момента импульса всей системы:
L_система = L_AB + L_CD

Таким образом, получен ответ на вопрос о моменте инерции и моменте импульса для данных систем.