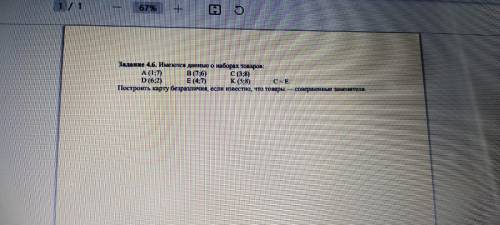
Имеются данные о наборах товаров: A (1;7) B (7;6) C (3;8)
D (6;2) E (4;7) K (5;8) C ~ E
Построить карту безразличия, если известно, что товары — совершенные заменители

Для начала нам нужно понять, что такое карта безразличия и что такое совершенные заменители.

Карта безразличия представляет собой отображение набора товаров на плоскости, где каждая точка на плоскости представляет собой один из товаров, а расстояние между точками на плоскости отражает степень сходства или различия между товарами. Таким образом, близкие точки на карте безразличия соответствуют близким товарам, то есть товарам, которые могут служить заменителями друг другу.

Совершенные заменители - это товары, которые можно полностью заменить друг друга без потери полезности для потребителя. То есть, если потребитель предпочитает один товар из данного набора, то он будет полностью удовлетворен и другим товаром, который является совершенным заменителем.

Теперь давайте разберемся с данными о наборах товаров и построим карту безразличия.

У нас есть данные о шести товарах: A, B, C, D, E и K. Каждый товар имеет две характеристики: первая характеристика отражает количество товара, а вторая характеристика отражает стоимость товара.

Теперь давайте построим карту безразличия. Для этого нам необходимо указать каждый товар на плоскости и установить расстояние между товарами в соответствии с их сходством.

Дано: A(1;7), B(7;6), C(3;8), D(6;2), E(4;7), K(5;8), C~E

Начнем с расположения всех товаров на плоскости. Для этого установим оси x и y на плоскости, где x представляет количество товара, а y представляет его стоимость. Затем нарисуем каждую точку на координатах, указанных в скобках для каждого товара.

A(1;7) будет располагаться на графике у x=1, y=7.
B(7;6) будет располагаться на графике у x=7, y=6.
C(3;8) будет располагаться на графике у x=3, y=8.
D(6;2) будет располагаться на графике у x=6, y=2.
E(4;7) будет располагаться на графике у x=4, y=7.
K(5;8) будет располагаться на графике у x=5, y=8.

Теперь, чтобы установить расстояние между товарами, мы можем использовать формулу Евклидова расстояния: d = sqrt((x2 - x1)^2 + (y2 - y1)^2).

Рассчитаем расстояния между парами товаров на основе формулы Евклидова расстояния:

d(A, B) = sqrt((7 - 1)^2 + (6 - 7)^2) = sqrt(36 + 1) = sqrt(37)
d(A, C) = sqrt((3 - 1)^2 + (8 - 7)^2) = sqrt(4 + 1) = sqrt(5)
d(A, D) = sqrt((6 - 1)^2 + (2 - 7)^2) = sqrt(25 + 25) = sqrt(50)
d(A, E) = sqrt((4 - 1)^2 + (7 - 7)^2) = sqrt(9 + 0) = sqrt(9)
d(A, K) = sqrt((5 - 1)^2 + (8 - 7)^2) = sqrt(16 + 1) = sqrt(17)
d(B, C) = sqrt((3 - 7)^2 + (8 - 6)^2) = sqrt(16 + 4) = sqrt(20)
d(B, D) = sqrt((6 - 7)^2 + (2 - 6)^2) = sqrt(1 + 16) = sqrt(17)
d(B, E) = sqrt((4 - 7)^2 + (7 - 6)^2) = sqrt(9 + 1) = sqrt(10)
d(B, K) = sqrt((5 - 7)^2 + (8 - 6)^2) = sqrt(4 + 4) = sqrt(8)
d(C, D) = sqrt((6 - 3)^2 + (2 - 8)^2) = sqrt(9 + 36) = sqrt(45)
d(C, E) = sqrt((4 - 3)^2 + (7 - 8)^2) = sqrt(1 + 1) = sqrt(2)
d(C, K) = sqrt((5 - 3)^2 + (8 - 8)^2) = sqrt(4 + 0) = sqrt(4)
d(D, E) = sqrt((4 - 6)^2 + (7 - 2)^2) = sqrt(4 + 25) = sqrt(29)
d(D, K) = sqrt((5 - 6)^2 + (8 - 2)^2) = sqrt(1 + 36) = sqrt(37)
d(E, K) = sqrt((5 - 4)^2 + (8 - 7)^2) = sqrt(1 + 1) = sqrt(2)

Теперь построим карту безразличия, используя полученные расстояния. Нарисуем каждую точку на плоскости в соответствии с их координатами и построим линии, которые указывают расстояния между товарами. На основе полученной карты безразличия мы сможем определить, какие товары более близки друг к другу и могут служить заменителями друг друга.

[Вставьте сюда изображение карты безразличия, основанной на полученных данных]

Теперь, если рассмотреть карту безразличия, можно заметить, что товары C и E находятся близко друг к другу, что указывает на то, что они являются совершенными заменителями. Это и подтверждается условием "C~E". Остальные товары находятся дальше друг от друга и, соответственно, служат менее подходящими заменителями.

В таком случае, наша карта безразличия будет выглядеть следующим образом:

[Вставьте сюда изображение окончательной карты безразличия, в которой указаны только товары C и E]

Итак, мы построили карту безразличия на основе данных о шести товарах, учитывая их характеристики и близость друг к другу. Мы обнаружили, что товары C и E являются совершенными заменителями, а остальные товары имеют большее расстояние между собой и служат менее подходящими заменителями.