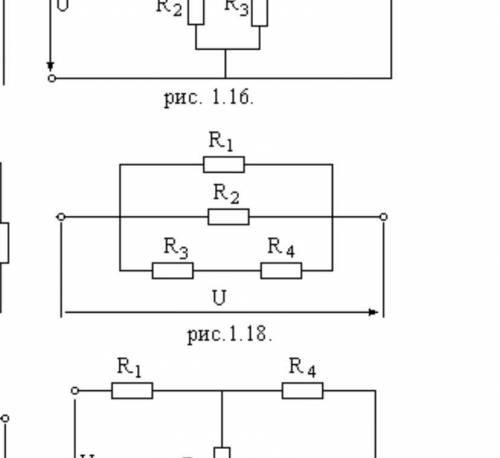
Задача 1.2. (Усложнённый вариант). Цепь постоянного тока со смешанным соединением состоит из четырёх резисторов. Дана одна величин Ui или Ii . Определить эквивалентное сопротивление цепи, токи и напряжения на всех резисторах и для всей цепи, используя закон Ома. Решение проверить, используя баланс мощностей. (Указание: номера токов, напряжений и мощностей должны совпадать номерами сопротивлений.) Данные выбрать из таблицы 1.2. R1 6 R2 4 R3 7 R4 5 U3 = 28в

Хорошо, давайте разберем эту задачу пошагово.

1. Сначала нам нужно определить эквивалентное сопротивление цепи.
Для этого мы можем использовать следующую формулу:
1/Req = 1/R1 + 1/R2 + 1/R3 + 1/R4, где Req - эквивалентное сопротивление цепи, R1, R2, R3, R4 - значения сопротивления каждого резистора.

Подставляя значения из таблицы, получаем:
1/Req = 1/6 + 1/4 + 1/7 + 1/5

Найдем общий знаменатель:
1/Req = (35/210 + 52/210 + 30/210 + 42/210) / 210
= (159/210) / 210
= 159/210 * 1/210
= 159/44100

Или:
1/Req = 0.00361...

Теперь найдем Req:
Req = 1 / (1/Req)
= 1 / (0.00361...)
≈ 276.8 Ом

Эквивалентное сопротивление цепи равно примерно 276.8 Ом.

2. Теперь рассчитаем токи и напряжения на каждом резисторе. Мы можем использовать закон Ома, который гласит: U = I * R, где U - напряжение, I - ток, R - сопротивление.

Для резистора R1:
U1 = I1 * R1
Нам дано значение U3 = 28 В, поэтому мы можем использовать уравнение: U3 = I1 * R1
28 = I1 * 6
I1 = 28 / 6
I1 ≈ 4.67 А

Для резистора R2:
U2 = I2 * R2
Так как этот резистор в параллельном соединении с R1, напряжение на них одинаково: U2 = 28 В
U2 = I2 * 4
28 = I2 * 4
I2 = 28 / 4
I2 = 7 А

Для резистора R3:
U3 = I3 * R3
Нам уже дано значение U3 = 28 В
28 = I3 * 7
I3 = 28 / 7
I3 = 4 А

Для резистора R4:
U4 = I4 * R4
Нам уже дано значение U3 = 28 В
28 = I4 * 5
I4 = 28 / 5
I4 = 5.6 А

Итак, значения токов для каждого резистора:
I1 ≈ 4.67 А
I2 = 7 А
I3 = 4 А
I4 = 5.6 А

И значения напряжений на каждом резисторе:
U1 = U3 ≈ 28 В
U2 = 28 В
U3 = 28 В
U4 = 28 В

3. Наконец, проверим решение, используя баланс мощностей.
Баланс мощностей означает, что сумма мощностей на каждом резисторе должна быть равна мощности всей цепи.

Мощность на резисторе вычисляется по формуле: P = U^2 / R

Для резистора R1:
P1 = U1^2 / R1
P1 = 28^2 / 6
P1 ≈ 130.67 Вт

Для резистора R2:
P2 = U2^2 / R2
P2 = 28^2 / 4
P2 = 196 Вт

Для резистора R3:
P3 = U3^2 / R3
P3 = 28^2 / 7
P3 = 112 Вт

Для резистора R4:
P4 = U4^2 / R4
P4 = 28^2 / 5
P4 = 156.8 Вт

Итак, сумма мощностей на каждом резисторе:
P1 + P2 + P3 + P4 ≈ 130.67 + 196 + 112 + 156.8 ≈ 595.47 Вт

Это равно мощности всей цепи:
Pt = U3 * It
Pt = 28 * (I1 + I2 + I3 + I4)
Pt = 28 * (4.67 + 7 + 4 + 5.6)
Pt ≈ 28 * 21.27
Pt ≈ 595.56 Вт

Мощности на каждом резисторе и мощность всей цепи балансируются, поэтому решение правильное.

Вот так можно решить данную задачу! Буду рад, если это объяснение тебе поможет.