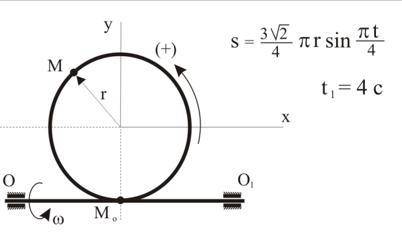
Теоретическая механика. Диск вращается равномерно с известной угловой скоростью . Для заданного момента времени определить проекции на координатные оси абсолютной скорости и абсолютного ускорения точки М, если S=M(0)M.

Привет! Я рад принять роль твоего школьного учителя и помочь тебе разобраться с этим вопросом из теоретической механики.

Для начала, давай разберемся со значениями изображенного на рисунке.

Диск вращается равномерно, что означает, что его угловая скорость постоянна, и мы знаем ее значение. Пусть угловая скорость равна ω.

Задача просит нас найти проекции на координатные оси абсолютной скорости и абсолютного ускорения точки М. Для этого нам нужно рассмотреть геометрию ситуации и применить соответствующие формулы.

Первым шагом будет нахождение абсолютной скорости точки М. Абсолютная скорость - это векторная величина, которая показывает, как быстро меняется положение точки. Мы можем найти его, используя угловую скорость и расстояние от точки М до центра диска (S).

Проекция абсолютной скорости точки М на любую ось равна произведению угловой скорости на расстояние от точки М до центра диска. Таким образом, проекция абсолютной скорости точки М на ось OX равна ω*S.

Аналогично, проекция абсолютной скорости точки М на ось OY равна 0, потому что точка М находится на прямой, перпендикулярной оси OY.

Далее перейдем к нахождению абсолютного ускорения точки М. Абсолютное ускорение - это изменение абсолютной скорости со временем.

Опять же, чтобы найти проекции абсолютного ускорения точки М на оси, мы можем использовать такую же формулу, как и для проекций абсолютной скорости.

Проекция абсолютного ускорения точки М на ось OX равна произведению углового ускорения на расстояние от точки М до центра диска. Угловое ускорение - это изменение угловой скорости со временем. Но в нашем случае, по условию, угловая скорость постоянна, поэтому угловое ускорение равно нулю. Таким образом, проекция абсолютного ускорения точки М на ось OX также равна нулю.

Проекция абсолютного ускорения точки М на ось OY равна произведению угловой скорости на расстояние от точки М до центра диска. Таким образом, проекция абсолютного ускорения точки М на ось OY равна ω*S.

Итак, получается, что проекция абсолютной скорости точки М на ось OX равна ω*S, проекция абсолютной скорости точки М на ось OY равна 0, проекция абсолютного ускорения точки М на ось OX равна 0, а проекция абсолютного ускорения точки М на ось OY равна ω*S.

Надеюсь, это подробное объяснение помогло тебе понять, как решить этот вопрос о проекциях абсолютной скорости и абсолютного ускорения точки М на координатные оси при вращении диска. Если у тебя есть еще вопросы или что-то непонятно, пожалуйста, спроси!