Признание ведущей роли механической формы движения материи и сведение более сложного - к простому, целого к сумме его частей

1. Подкоренное выражение неотрицательно, знаменатель не равен 0

обьединяя

2. Область определения - множество всех действительных чисел, x є R

по определению функция g(x) нечетная

3.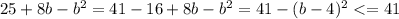 , причем равенство достигается при b=4

(так как квадрат любого выражения неотрицателен)

4. График во вложении

при x>=0 график имеет вид y=x^2-8x+13 вершина параболы (4;-3)

при x<0 график имеет вид y=x^2+8x+13 вершина параболы (-4;-3)

5. 2х-1=0

х=0.5 - вертикальная асимптота

ищем наклонные асимптоты

значит наклонная будет одновременно горизонтальной асимптотой и равна y=-3

6. График во вложении

 Область определения D(y)=R

Область значений функций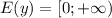

Функция четная, непериодичная

Функция положительная на R/{-2;2}

Нули функции х1=-2, х2=2

Функция убывает на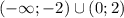

Функция возростает на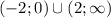

х=-2 и х=2 - точки локального минимума (y(-2)=y(2)=0)

x=0 - точка локального максимума (y(0)=4)

Асимптот функция не имеет