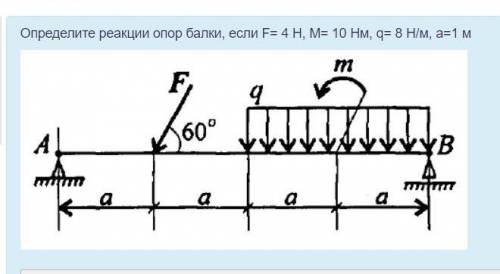
Определите реакции опор балки, если F= 4 H, M= 10 Hм, q= 8 H/м, a=1 м

Чтобы определить реакции опор балки, нам необходимо анализировать силы, моменты и равновесие системы.

Для начала, давайте определим известные величины:
- F = 4 H (сила, действующая на балку)
- M = 10 Hм (момент относительно опоры В)
- q = 8 H/м (распределенная нагрузка на балку)
- a = 1 м (расстояние от опоры А до опоры В)

Для решения данной задачи, мы будем использовать два основных принципа механики: равновесие сил и равновесие момента.

1. Равновесие сил:
Сумма вертикальных сил должна равняться нулю, поскольку балка находится в состоянии равновесия. Изображение показывает, что две опоры обеспечивают вертикальную реакцию, R_A и R_B. С учетом распределенной нагрузки q и силы F, мы можем записать следующее уравнение:
ΣF_y = R_A + R_B - F - q * a = 0

2. Равновесие момента:
Сумма моментов относительно любой точки должна равняться нулю. Давайте возьмем точку А (левую опору) в качестве точки, где мы хотим рассмотреть моменты. Тогда момент от силы F будет равен 0, поскольку она проходит через эту точку. Момент от распределенной нагрузки будет равен q * a * (a/2), поскольку она создает равномерное распределение на половине расстоянии a. Момент от силы реакции R_B будет равен R_B * a, поскольку он создает момент относительно точки А.
ΣM_A = R_B * a - q * a * (a/2) - M = 0

Теперь у нас есть два уравнения: ΣF_y = 0 и ΣM_A = 0. Мы можем решить их, чтобы определить реакции опор балки R_A и R_B.

Решение:
1. Равновесие сил:
R_A + R_B - F - q * a = 0
R_A + R_B = F + q * a

2. Равновесие момента:
R_B * a - q * a * (a/2) - M = 0
R_B * a = q * a * (a/2) + M
R_B = (q * a^2 / 2 + M) / a

Теперь мы можем заменить R_B в уравнении равновесия сил:

R_A + (q * a^2 / 2 + M) / a = F + q * a
R_A a + q * (a^2 / 2 + M / a) = a * F + q * a^2

Упрощая, получим:

R_A = a * F - q * a^2 + q * (a^2 / 2 + M / a)

Теперь мы можем подставить значения F = 4 H, M = 10 Hм, q = 8 H/м и a = 1 м:

R_A = 1 * 4 - 8 * 1 + 8 * (1^2 / 2 + 10 / 1)
R_A = 4 - 8 + 8 * (1/2 + 10)
R_A = 4 - 8 + 88
R_A = -4 + 88
R_A = 84 H

Теперь мы знаем, что R_A равно 84 H. Чтобы найти R_B, мы можем использовать уравнение равновесия момента:

R_B = (q * a^2 / 2 + M) / a
R_B = (8 * 1^2 / 2 + 10) / 1
R_B = (8/2 + 10) / 1
R_B = (4 + 10) / 1
R_B = 14 H

Таким образом, реакция опоры А (R_A) равна 84 H, а реакция опоры В (R_B) равна 14 H.