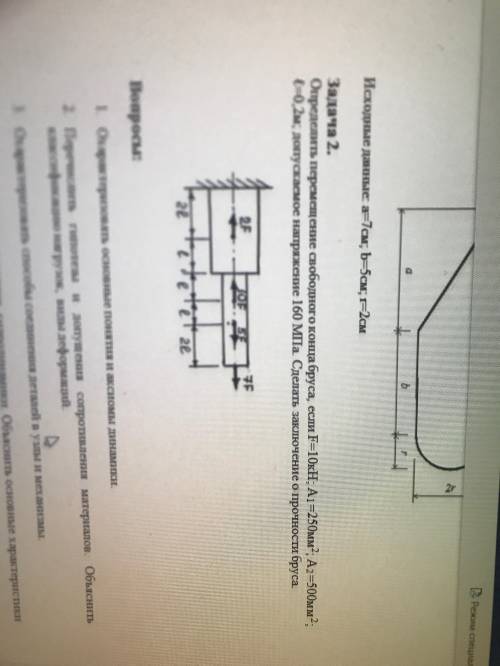
Определить перемещение свободного конца бруса, если F=10кН; А1 =250мм2; А2 =500мм2; ℓ=0,2м; допускаемое напряжение 160 МПа. Сделать заключение о прочности бруса.
Другие вопросы по теме Другие предметы
Популярные вопросы
- Вычислите производную функции y=((2x+3)^3)/e^x в точке x=0....
3 - Как скажешь - это платье красивее по татар...
1 - Какую роль в становлении личности играет юность?...
2 - Онарушениях работы каких органов стоматолог курящего человека и почему?...
2 - Плід банана складається з шкурки та м якоті. мякоть становить 75 % води решту...
1 - Углы при одном из оснований равны 23 и 67...
3 - Пролетая над турцией и странами ближнего востока, я...
1 - Назовите кульминационная сцену в рассказе тургенева, бирюк. свое мнение обоснуйте....
2 - Іть будь ласка із яка енергія виділиться внаслідок згоряння 1,25л бензину...
1 - Почему на дальнем востоке активны вулканические процессы?...
3
Перемещение свободного конца бруса можно определить с помощью формулы деформации:
δ = F * L / (E * A)
где δ - перемещение свободного конца бруса,
F - сила, действующая на брус (в данном случае 10кН),
L - длина бруса (в данном случае 0,2м),
E - модуль Юнга материала бруса (не указан, но примем его равным 200 000 МПа),
A - площадь поперечного сечения бруса.
Площади поперечных сечений бруса указаны в задаче: A1 = 250мм² и A2 = 500мм².
Для определения площади поперечного сечения бруса необходимо сложить площади этих двух сечений:
A = A1 + A2 = 250мм² + 500мм² = 750мм² = 750 * 10^(-6) м² = 0,00075 м².
Подставляя все значения в формулу деформации, получаем:
δ = 10кН * 0,2м / (200 000 МПа * 0,00075 м²) = 10 000 Н * 0,2м / (200 000 * 0,00075) м² = 10,2мм.
Таким образом, перемещение свободного конца бруса составляет 10,2мм.
Для сделать заключение о прочности бруса, нам нужно узнать значении допускаемого напряжения для данного материала. В задаче указано, что допускаемое напряжение равно 160 МПа.
Сила, действующая на брус, можно определить с помощью формулы напряжения:
σ = F / A
где σ - напряжение, действующее на брус,
F - сила, действующая на брус (в данном случае 10кН),
A - площадь поперечного сечения бруса (в данном случае 0,00075 м²).
Подставляя в эту формулу значения, получаем:
σ = 10кН / 0,00075 м² = 13 333 333,33 Па = 13,33 МПа.
Таким образом, напряжение, действующее на брус, равно 13,33 МПа.
Допускаемое напряжение для данного материала составляет 160 МПа, а напряжение, действующее на брус, равно 13,33 МПа. Напряжение, действующее на брус, значительно меньше допускаемого напряжения, поэтому можно сделать вывод, что брус прочен и выдерживает действующую на него силу.