Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.
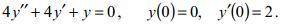
Другие вопросы по теме Другие предметы
Популярные вопросы
- In uzbekistan all the documents at all offices and state bodies...
2 - Iwas cooking dinner, i cut my finger. a) while b) since c) during...
3 - Выберите наиболее общую характеристику ресурсов. 1)альтернотивность....
1 - It is a well-known fact that william shakespeare was both a playwright...
3 - Решите систему уравнений 2x+3x=1 6x-2y=14...
3 - Все past simple и паст континиос...
3 - Вкоробке есть 50 бутылок, половина из них с красной этикеткой,...
3 - Решить уравнение (икс в кубе и в квадрате) x^3+5x^2-x-5=0...
3 - Эссе на тему современные педагогические технологии дошкольного...
3 - Никонами и старобоярцами называли сторонников и противников чего...
1
Объяснение:
4y" + 4y' + y = 0, y(0) = 0, y'(0) = 2
Данное уравнение является линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами.
Запишем характеристическое уравнение
4k² + 4k + 1 = 0
(2k + 1)² = 0
k₁ = k₂ = -0,5
поэтому общее решение дифференциального уравнения выражается формулой
Подставим начальные условия и найдем константы С₁ и С₂
y(0) = 0
Поэтому С₁ =0
y'(0) = 2
Найдем производную функции
Запишем частное решение уравнения