1. Другие предметы
  2. Log (основание 0,1) от

Log (основание 0,1) от (х^2-3х+3)=х^2-3х+2 найти сумму квадратов корней уравнения

Vitalihka Vitalihka    2   02.08.2020 22:07    0

Ответы
машуня89 машуня89  15.10.2020 15:39

5

Объяснение:

Ограничение: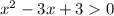 x^2-3x+30

________________________

log_{0.1}(x^2-3x+3)=x^2-3x+2\\ \left[x^2-3x+3=t\right]\\ \underbrace{log_{0.1}t}_{f(t)}=\underbrace{t-1}_{g(t)}

Основание логарифма 0.1<1, а значит f(x) монотонно убывает. g(x) - прямая, причем тангенс угла наклона равен 1>0 => g(x) монотонно возрастает => графики имеют не более одной точки пересечения. Нетрудно отыскать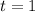 t=1

Возвращаемся к исходной переменной:

x^2-3x+3=1\\ x^2-3x+2=0\\ \left[x_1+x_2=3,x_1x_2=2\right]\\ x=1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x=2

1^2+2^2=5

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Другие предметы
ник4774 ник4774  04.12.2020 10:05
Назовите причины перехода к кочевому животноводству 1. причина 2. причина 3 причина...
milayakisa1 milayakisa1  04.12.2020 10:05
Нужен парень лет 12 -15 пешите номер 89082965508 ватсап и вк...
Ychenik1354 Ychenik1354  04.12.2020 10:07
ТЕХНОЛОГИЯ ответить на вопросы письменно. 1. Что Такое деталировка? 2. Что указывается в технологической карте? 3. Из каких этапов состоит технологический процесс изготовления детали...
noybet444noybet noybet444noybet  04.12.2020 10:19
Сколько видов включает в себясколько видов включает в себя женская гимнастическое многоборье ​...
nadyushka3 nadyushka3  04.12.2020 10:19
Дил баян Айлана- чөйрө Тууранды сөздөр менен...
Нннннннн11 Нннннннн11  24.11.2020 07:48
Пацаны там дз про детство Л.Н.Толстой короче (короче это мало) текста что бы я запомнил...
nastyassddffgbvgg nastyassddffgbvgg  24.11.2020 07:49
10 одсту про опу і опору сори. 8) Реши уравнения.1000 – х = 35 + 6 - 881: y = 63 : 7х: 8 = 100 - (49)​...
lora1981 lora1981  06.10.2020 11:52
Проанализируй источник. Установи правильную взаимосвязь документа и его названия. «2 ноября... Байков переправился на Иртыш, где стояли каменные палаты, вверх по Иртышу, лежащее,где...
HelpMePlsIs HelpMePlsIs  06.10.2020 11:52
Почему когда в диалоге нажимаешь на картинку которую отправил собеседник,когда нажимаешь не на лайки а на значок коментарий написать,пишет ошибка,это что значит,что собеседник удалил...
saule19611225 saule19611225  12.04.2021 00:38
Help me please Нужно сдать,а времени почти не осталось...

Популярные вопросы