Движение материальной точки массойm=8кг происходит в горизонтальной плоскости Оxy согласно уравнениям x=0,05 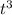
и y=0,3
Оприделить модуль равнодействующей приложенных к точке сил в момент времени t=4с
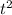
Другие вопросы по теме Другие предметы
Популярные вопросы
- 6. Наведіть факти, що свідчать про виснаження воюючих сторін...
1 - Користуючись даним планом, скласти історичний портрет одного з діячів Великої...
1 - MgS найдите в каком соотношении реагируют магний и сера . Сколько потребуется...
2 - Кристаллогидрат нитрата алюминия содержит по массе 76,8% кислорода. Выведите...
1 - Розберіть за будовою та укажіть б словотворення лексеми ПАДОЛИСТ...
2 - 1-тапсырма. Сұрақтарға жауап беріңдер: «Қоғамға қызмет ету» дегенді қалай түсінесің?...
1 - В то время, как на водопой отправился находящийся в 6 минутах от него один львёнок,...
1 - Великие математики сего привлекательного мира подскажите биологу как это решать:...
1 - 10 ВОПРОСОВ 1. Как проходила жизнь Кирилы Петровича Троекурова?2. Что послужило...
3 - Отгадай загадки: 1: Рыбки плавали, ныряли, В прятки весело играли. Но однажды...
2
Уравнение движения x(t) = 0,05t^3 и y(t) = 0,3t^2 дают зависимость координаты точки от времени t. Чтобы найти скорость и ускорение точки, необходимо продифференцировать эти уравнения по времени:
v_x(t) = d(x(t))/dt = d(0,05t^3)/dt = 3*0,05t^2 = 0,15t^2
v_y(t) = d(y(t))/dt = d(0,3t^2)/dt = 2*0,3t = 0,6t
a_x(t) = d(v_x(t))/dt = d(0,15t^2)/dt = 0,3t
a_y(t) = d(v_y(t))/dt = d(0,6t)/dt = 0,6
Теперь найдем равнодействующую силу в каждом направлении. Равнодействующая сила в направлении Ox будет равна проекции ускорения на эту ось:
F_x = m*a_x(t) = 8*0,3t = 2,4t
Равнодействующая сила в направлении Oy будет равна проекции ускорения на эту ось:
F_y = m*a_y(t) = 8*0,6 = 4,8
Теперь мы можем найти модуль равнодействующей силы:
F = sqrt(F_x^2 + F_y^2) = sqrt((2,4t)^2 + (4,8)^2) = sqrt(5,76t^2 + 23,04)
Теперь подставим t = 4 секунды:
F = sqrt(5,76*4^2 + 23,04) = sqrt(92,16 + 23,04) = sqrt(115,2) ≈ 10,73 Н
Таким образом, модуль равнодействующей силы приложенных к точке в момент времени t = 4с составляет около 10,73 Н (ньютонов).