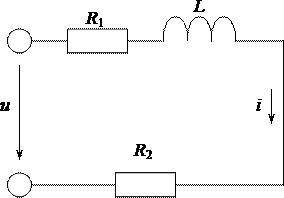
Дано: u = 564 sin ωt; R1=8 Ом; R2=8 Ом; L=0,0383 Гн; f=50 Гц. Определить: I; S; P; Q. Построить векторную диаграмму.
3 ВАРИАНТ .

НУЖНО

Для решения данной задачи, нам необходимо использовать формулы, связанные с электрическим током, мощностью и реактивной мощностью в электрической цепи.

По условию дано следующие данные:
u = 564 sin ωt - напряжение в цепи
R1 = 8 Ом - сопротивление первого резистора
R2 = 8 Ом - сопротивление второго резистора
L = 0,0383 Гн - индуктивность катушки
f = 50 Гц - частота сигнала

1. Определение тока I:
Для определения тока I, используем закон Ома: I = U / Z, где U - напряжение, а Z - импеданс.
Так как в цепи присутствует не только сопротивление, но и индуктивность, то нужно представить импеданс в виде вектора.
Импеданс индуктивного элемента в цепи можно определить по формуле: ZL = jωL, где ω = 2πf - угловая частота, j - мнимая единица.
Импеданс для резисторов R1 и R2 просто равен их сопротивлениям: ZR = R.

Теперь суммируем импедансы всех элементов цепи: Z = ZR1 + ZR2 + ZL
Z = R1 + R2 + jωL
Z = 8 + 8 + j*2π*50*0,0383
Z = 16 + j12,14 Ом

Подставляем значение напряжения u = 564 sin ωt:
I = U / Z = (564 sin ωt) / (16 + j12,14)

2. Определение полной мощности S:
Полная мощность S в электрической цепи можно вычислить по формуле:
S = β * Z*, где Î - комплексное сопротивление, Z* - сопряженное значение импеданса.

Вычисляем комплексное сопротивление:
Î = I * √2 = (564 sin ωt) / (16 + j12,14) * √2

Вычисляем сопряженное значение импеданса:
Z* = R* + jX* = R - jX = 16 - j12,14

Теперь, подставляем значения β и Z* в формулу:
S = (β) * Z* = ((564 sin ωt) / (16 + j12,14))^2 * (16 - j12,14)

3. Определение активной мощности P:
Активная мощность P в электрической цепи может быть найдена по формуле:
P = Re(S), где Re - оператор, возвращающий действительную часть комплексного числа.

Подставляем значение S и вычисляем Re(S) для определения активной мощности P.

4. Определение реактивной мощности Q:
Реактивная мощность Q может быть найдена по формуле:
Q = Im(S), где Im - оператор, возвращающий мнимую часть комплексного числа.

Подставляем значение S и вычисляем Im(S) для определения реактивной мощности Q.

5. Построение векторной диаграммы:
Для построения векторной диаграммы используем комплексный вектор напряжения и комплексный вектор тока.
Найденный ранее комплексный вектор напряжения равен U / √2, где U - напряжение.
Комплексный вектор тока равен Î.
Строим векторные диаграммы и измеряем их длины, углы и направления.

Надеюсь, данное решение было понятно для вас. Если у вас возникнут еще вопросы, не стесняйтесь задавать!